
(1)求φ;
(2)求函数y=f(x)的单调增区间;
(3)画出函数y=f(x)在区间[0,π)上的图象;
(4)此函数图象如何由y=sinx图象变化得到?
思路分析:对称轴必经过三角函数的最高点或最低点,即f(![]() )=±1,由此求出φ,后面的问题就可获解.
)=±1,由此求出φ,后面的问题就可获解.
解:(1)∵x=![]() 是函数y=f(x)的图象的对称轴,
是函数y=f(x)的图象的对称轴,
∴sin(2×![]() +φ)=±1.∴
+φ)=±1.∴![]() +φ=kπ+
+φ=kπ+![]() ,k∈Z.
,k∈Z.
∵-π<φ<0,∴φ=-![]() .
.
(2)由(1)知φ=-![]() ,因此y=sin(2x-
,因此y=sin(2x-![]() ).
).
由题意得2kπ-![]() ≤2x-
≤2x-![]() ≤2kπ+
≤2kπ+![]() ,k∈Z.
,k∈Z.
∴函数y=sin(2x-![]() )的单调增区间为[kπ+
)的单调增区间为[kπ+![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
(3)由y=sin(2x-![]() )知
)知
x | 0 |
|
|
|
| π |
y |
| -1 | 0 | 1 | 0 |
|
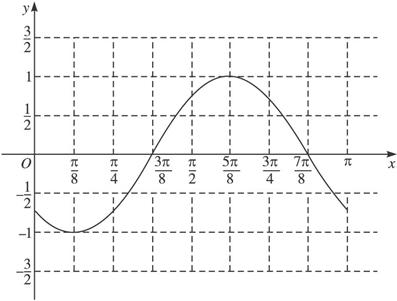
故函数y=f(x)在区间[0,π]上的图象是

(4)将y=sinx的图象向右平移![]() 个单位,得到y=sin(x
个单位,得到y=sin(x![]() )的图象,然后将图象上各点的横坐标缩短为原来的
)的图象,然后将图象上各点的横坐标缩短为原来的![]() 倍(纵坐标不变),得到函数y=sin(2x
倍(纵坐标不变),得到函数y=sin(2x![]() )的图象.
)的图象.
另解:先将y=sinx的图象上各点的横坐标缩短为原来的![]() 倍,变为y=sin2x的图象,再将图象向右平移
倍,变为y=sin2x的图象,再将图象向右平移![]() 个单位,得到y=sin[2(x-
个单位,得到y=sin[2(x-![]() )]=sin(2x
)]=sin(2x![]() )的图象.
)的图象.
思想方法小结:利用函数的对称性解题,通过数形结合得到方程,根据已知条件确定相应的φ值,这是本题的关键.画图象要视问题的情况,灵活使用“描点法”或“五点法”.


科目:高中数学 来源: 题型:
| π |
| 6 |
| x |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 设函数f(x)=sin(ωx+
设函数f(x)=sin(ωx+| π |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| ωx |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com