两个函数y=x-1与y=lnx的图象共有公共点 个.
【答案】
分析:两个函数图象公共点的问题,可以转化为方程x-1-lnx=0的解的个数问题,进而研究函数y=x-1-lnx的单调性和值域问题,利用导数研究它的单调性,不难得出最小值为0,因此可得答案.
解答:解:求两个函数y=x-1与y=lnx的图象共有公共点,
即为求方程x-1-lnx=0的解的个数
记函数G(x)=x-1-lnx (x>0)
可得G′(x)=1-
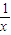
=
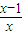
当x∈(0,1)时,G′(x)<0,函数G(x)为减函数;
当x∈(1,+∞)时,G′(x)>0,函数G(x)为增函数
所以函数G(x)的最小值为G(1)=0
因此方程x-1-lnx=0的解的个数为零.
即两个函数的图象只有一个公共点.
所以答案为:1
点评:本题考查了函数图象的有关知识,属于基础题.将函数图象的公共点问题转化为方程问题,再用导数研究新的函数的零点,是解决本题的关键.

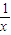 =
=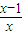


 阅读快车系列答案
阅读快车系列答案