
 |x|在x∈[-1,1]的图象上有两点A,B,AB∥Ox轴,点M(1,m)(m是已知实数,且m>
|x|在x∈[-1,1]的图象上有两点A,B,AB∥Ox轴,点M(1,m)(m是已知实数,且m> )是△ABC的边BC的中点.
)是△ABC的边BC的中点.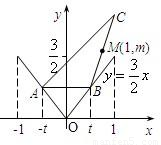
 t),A(-t,
t),A(-t, t)(t>0),C(x,y).求出△ABC中边|AB|及AB边上的高h,再利用三角形的面积公式计算即得;
t)(t>0),C(x,y).求出△ABC中边|AB|及AB边上的高h,再利用三角形的面积公式计算即得;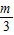 )2+
)2+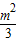 ,t∈(0,1].下面结合二次函数的图象与性质求解其最大值即可.
,t∈(0,1].下面结合二次函数的图象与性质求解其最大值即可. t),A(-t,
t),A(-t, t)(t>0),C(x,y).
t)(t>0),C(x,y).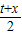 =1,
=1, =m,∴x=2-t,y=2m-
=m,∴x=2-t,y=2m- t.
t. t=2m-3t.
t=2m-3t. |AB|•h=
|AB|•h= •2t•(2m-3t)=-3t2+2mt,t∈(0,1].
•2t•(2m-3t)=-3t2+2mt,t∈(0,1].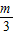 )2+
)2+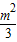 ,t∈(0,1].若
,t∈(0,1].若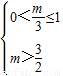 ,
, <m≤3.当t=
<m≤3.当t=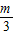 时,Smax=
时,Smax=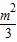 ,相应的C点坐标是(2-
,相应的C点坐标是(2-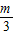 ,
, m).
m).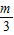 >1,即m>3时,S=f(t)在区间(0,1]上是增函数,
>1,即m>3时,S=f(t)在区间(0,1]上是增函数, ).
).

科目:高中数学 来源: 题型:
如图,函数y=![]() |x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>
|x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>![]() )是△ABC的BC边的中点.
)是△ABC的BC边的中点.
(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);
(2)求函数S=f(t)的最大值,并求出相应的C点坐标.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第一次月考理科数学试卷 题型:解答题
(本小题12分)如图,函数y= |x|在x∈[-1,1]的图象上有两点A、B,AB∥
|x|在x∈[-1,1]的图象上有两点A、B,AB∥
Ox轴,点M(1,m)(m是已知实数,且m> )是△ABC的边BC的中点。
)是△ABC的边BC的中点。
(Ⅰ)写出用B的横坐标t表示△ABC面积S的函数解析式S=f(t);
(Ⅱ)求函数S=f(t)的最大值,并求出相应的C点坐标。

查看答案和解析>>
科目:高中数学 来源:2009-2010学年数学寒假作业(09)(解析版) 题型:解答题
 ).
). ;②xy=9;③xy=
;②xy=9;③xy= .请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;
.请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长; x+
x+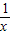 的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com