已知长方体的侧面积为6,高为1,则长方体对角线长的最小值为 ________.
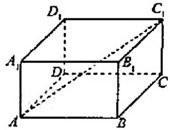
分析:先设AA
1=1,AB=a,AD=b,利用题中条件:“侧面积为6”建立关于a,b的等式,再根据长方体对角线长定理用a,b表示出对角线AC
1的长,最后利用基本不等式求出它的最小值即可.
解答:
解:设AA
1=1,AB=a,AD=b,
则2(a+b)×1=6,∴a+b=3
又对角线AC
12=a
2+b
2+c
2=1+a
2+b
2+≥1+
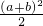
=1+

=

,
则长方体对角线长的最小值为
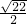
,
故答案为:
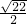
.
点评:本题主要考查了点、线、面间的距离计算、基本不等式,考查空间想象能力、运算能力和推理论证能力,属于基础题.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案