
(13分)
在平面直角坐标系xOy中,抛物线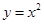 上异于坐标原点O的两不同动点A、B满足
上异于坐标原点O的两不同动点A、B满足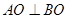 (如图所示).
(如图所示).
(Ⅰ)求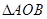 得重心G(即三角形三条中线的交点)的轨迹方程;
得重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)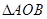 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
(07年重庆卷理)(13分)
如图,在直三棱柱ABC―![]() 中,
中,![]() AB = 1,
AB = 1,![]() ;点D、E分别在
;点D、E分别在![]() 上,且
上,且![]() ,四棱锥
,四棱锥![]() 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与![]() 的距离;(8分)
的距离;(8分)
(2)若BC =![]() ,求二面角
,求二面角![]() 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年重庆卷理)(13分)
如图,在直三棱柱ABC―![]() 中,
中,![]() AB = 1,
AB = 1,![]() ;点D、E分别在
;点D、E分别在![]() 上,且
上,且![]() ,四棱锥
,四棱锥![]() 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与![]() 的距离;(8分)
的距离;(8分)
(2)若BC =![]() ,求二面角
,求二面角![]() 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
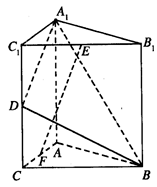 (本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷十二文科数学 题型:解答题
(本小题满分13分)
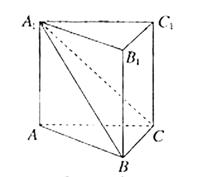 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
(Ⅰ)求证:AB⊥BC;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ.判断θ与φ的大小关系,并予以证明.
查看答案和解析>>
科目:高中数学 来源:2010年北京东城区高三上学期理科数学综合练习(一) 题型:解答题
(本小题满分13分)
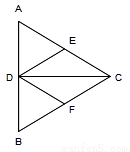
正△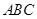 的边长为4,
的边长为4,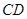 是
是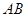 边上的高,
边上的高,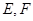 分别是
分别是 和
和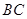 边的中点,现将△
边的中点,现将△ 沿
沿 翻折成直二面角
翻折成直二面角 .
.
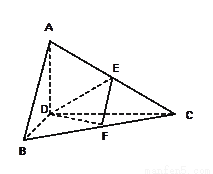
(1)试判断直线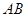 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角 的余弦值;
的余弦值;
(3)在线段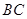 上是否存在一点
上是否存在一点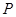 ,使
,使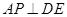 ?证明你的结论.
?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com