
分析 (1)从问题的反面进行解答,只要除去没有女生的部分;
(2)由题意求出二项展开式的第三项,得到关于n 的方程,然后利用通项公式求二项式系数最大项.
解答 解:(1)从5位男生与3位女生中选派4名代表参加某项活动,共有${C}_{9}^{4}$种不同的选法,
而没有女生的选法有${C}_{5}^{4}$,所以其中至少有1位女生的选派方案有${C}_{9}^{4}-{C}_{5}^{4}$=121;
(2)因为($\sqrt{x}$-$\frac{2}{x}$)n的展开式中x的一次项是第3项,
所以${C}_{n}^{2}(\sqrt{x})^{n-2}(-\frac{2}{x})^{2}$=$(-2)^{2}{C}_{n}^{2}{x}^{\frac{n-4}{2}}$,所以n=6,
所以展开式中二次项系数最大的项为第四项,即${T}_{4}={C}_{6}^{3}(\sqrt{x})^{3}(-\frac{2}{x})^{3}=-160{x}^{-\frac{3}{2}}$.
点评 本题考查了组合的应用以及二项展开式定理的运用;属于基础题.


科目:高中数学 来源: 题型:填空题
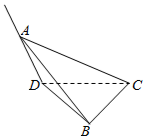 如图,在二面角A-CD-B中,BC⊥CD,BC=CD=2,点A在直线AD上运动,满足AD⊥CD,AB=3.现将平面ADC沿着CD进行翻折,在翻折的过程中,线段AD长的取值范围是$[\sqrt{5}-2,\sqrt{5}+2]$.
如图,在二面角A-CD-B中,BC⊥CD,BC=CD=2,点A在直线AD上运动,满足AD⊥CD,AB=3.现将平面ADC沿着CD进行翻折,在翻折的过程中,线段AD长的取值范围是$[\sqrt{5}-2,\sqrt{5}+2]$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{4}$) | B. | (-1,$\frac{1}{2}$)∪(1,+∞) | C. | (-∞,-1)∪(4,+∞) | D. | (-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (1,3) | C. | (-1,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 未服用药 | 25 | 15 | 40 |
| 服用药 | c | d | 40 |
| 总计 | M | N | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (1,2)与(2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com