
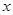 、
、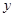 满足约束条件
满足约束条件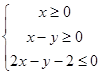 ,则
,则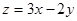 的最大值为 ________.
的最大值为 ________.科目:高中数学 来源:不详 题型:解答题
| | 产品A(件) | 产品B(件) | |
| 研制成本与搭载 费用之和(万元/件) | 20 | 30 | 计划最大资金额300万元 |
| 产品重量(千克/件) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元/件) | 80 | 60 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com