
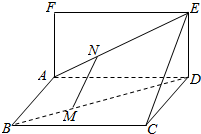
 如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD、AE上,且BM=$\frac{1}{3}$BD,AN=$\frac{1}{3}$AE,求证:MN∥平面CDE.
如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD、AE上,且BM=$\frac{1}{3}$BD,AN=$\frac{1}{3}$AE,求证:MN∥平面CDE. 分析 由$\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{AN}$=$\frac{2}{3}\overrightarrow{CD}+\frac{1}{3}\overrightarrow{DE}$,能证明MN∥平面CDE.
解答  证明:因为M 在BD 上,且BM=$\frac{1}{3}BD$,
证明:因为M 在BD 上,且BM=$\frac{1}{3}BD$,
所以$\overrightarrow{MB}=\frac{1}{3}\overrightarrow{DB}=\frac{1}{3}\overrightarrow{DA}+\frac{1}{3}\overrightarrow{AB}$,
同理$\overrightarrow{AN}$=$\frac{1}{3}\overrightarrow{AD}+\frac{1}{3}\overrightarrow{DE}$,
所以$\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{AN}$=($\frac{1}{3}\overrightarrow{DA}+\frac{1}{3}\overrightarrow{AB}$)+$\overrightarrow{BA}$+($\frac{1}{3}\overrightarrow{AD}+\frac{1}{3}\overrightarrow{DE}$)=$\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{DE}$=$\frac{2}{3}\overrightarrow{CD}+\frac{1}{3}\overrightarrow{DE}$,
又$\overrightarrow{CD}$与$\overrightarrow{DE}$不共线,根据向量共面的充要条件可知$\overrightarrow{MN},\overrightarrow{CD},\overrightarrow{DE}$共面,
由于MN不在平面CDE内,所以MN∥平面CDE.
点评 本题考查线面平行的证明,是基础题,解题时要认真审题,注意向量法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 132 | B. | 66 | C. | 48 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | C. | $[-\frac{{\sqrt{3}}}{2},1]$ | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | θn随着n的增大而增大 | B. | θn随着n的增大而减小 | ||
| C. | 随着n的增大,θn先增大后减小 | D. | 随着n的增大,θn先减小后增大 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -1 | C. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
| A. | -11 | B. | -2 | C. | 1 | D. | -5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com