
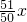 -ax2,x∈[t,+∞),其中t为大于
-ax2,x∈[t,+∞),其中t为大于 的常数.当x=10万元时,y=9.2万元,又每投入x万元需缴纳(3+ln
的常数.当x=10万元时,y=9.2万元,又每投入x万元需缴纳(3+ln )万元的增值税(旅游增加值=旅游收入-增值税).
)万元的增值税(旅游增加值=旅游收入-增值税).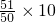 -100a=9.2,∴a=
-100a=9.2,∴a=
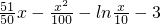 ,x∈[t,+∞),
,x∈[t,+∞),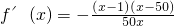
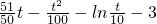
 时,x∈(t,1),f′(x)<0,f(x)单调递减;x∈(1,50),f′(x)>0,f(x)单调递增;x∈(50,+∞)时,f′(x)<0,f(x)单调递减
时,x∈(t,1),f′(x)<0,f(x)单调递减;x∈(1,50),f′(x)>0,f(x)单调递增;x∈(50,+∞)时,f′(x)<0,f(x)单调递减 )>f(t),M=f(50)=23-ln5
)>f(t),M=f(50)=23-ln5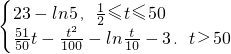


 优加精卷系列答案
优加精卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com