
如图所示,在直角坐标系xOy中,点P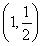 到抛物线C:y2=2px(p>0)的准线的距离为
到抛物线C:y2=2px(p>0)的准线的距离为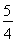 .点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
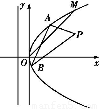
(1)求p,t的值;
(2)求△ABP面积的最大值.
(1)  (2)
(2) 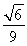
【解析】
解:(1)由题意知 得
得
(2)由(1)知M(1,1),
直线OM的方程为y=x,
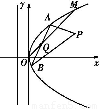
设A(x1,y1),B(x2,y2),线段AB的中点为Q(m,m).
由题意知,
设直线AB的斜率为k(k≠0).
由
得(y1-y2)(y1+y2)=x1-x2,
故k·2m=1,
所以直线AB的方程为y-m=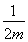 (x-m),
(x-m),
即x-2my+2m2-m=0.
由 消去x,
消去x,
整理得y2-2my+2m2-m=0,
所以Δ=4m-4m2>0,
y1+y2=2m,y1y2=2m2-m.
从而|AB|=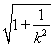 ·|y1-y2|=
·|y1-y2|= ·
· .
.
设点P到直线AB的距离为d,
则d= .
.
设△ABP的面积为S,则
S=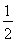 |AB|·d=|1-2(m-m2)|·
|AB|·d=|1-2(m-m2)|·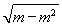 .
.
由Δ=4m-4m2>0,得0<m<1.
令u=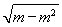 ,0<u≤
,0<u≤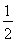 ,则S=u(1-2u2).
,则S=u(1-2u2).
设S(u)=u(1-2u2),0<u≤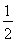 ,则S′(u)=1-6u2.
,则S′(u)=1-6u2.
由S′(u)=0,得u=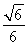 ∈
∈ ,
,
因此S(u)在 单调递增,在
单调递增,在 单调递减,
单调递减,
所以S(u)max=S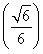 =
=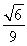 .
.
故△ABP面积的最大值为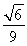 .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
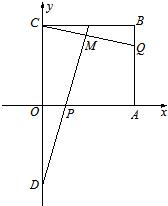 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,| OC |=
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,| OC |=| 3 |
| OP |
| λOA |
| AQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
(2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.查看答案和解析>>
科目:高中数学 来源:2010年湖南省高考适应性测试数学试卷(文科)(解析版) 题型:解答题
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
查看答案和解析>>
科目:高中数学 来源:2010年高考数学模拟试卷(文科)(解析版) 题型:解答题
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省连云港市东海高级中学高考数学考前猜题试卷(1)(解析版) 题型:解答题
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com