
(1)写出其中次品数ξ的分布列;
(2)求P(ξ≥1).
分析:本题考查二项分布的概率分布公式和某些简单的离散型随机变量的分布列以及由分布列求出一些事件的概率.这是n次独立重复试验,出现次品数ξ服从二项分布,由概率公式P(ξ=k)=![]() pkqn-k(0<p<1,p+q=1且k=0,1,2,…,n)就可求出ξ的分布列,从而求出P(ξ≥1).
pkqn-k(0<p<1,p+q=1且k=0,1,2,…,n)就可求出ξ的分布列,从而求出P(ξ≥1).
解:依题意,随机变量ξ&B(2,5%).
P(ξ=0)=![]() (95%)2=0.902 5,
(95%)2=0.902 5,
P(ξ=1)=![]() (5%)(95%)=0.095,
(5%)(95%)=0.095,
P(ξ=2)=![]() (5%)2=0.002 5.
(5%)2=0.002 5.
因此,
(1)次品数ξ的分布列是
ξ | 0 | 1 | 2 |
P | 0.902 5 | 0.095 | 0.002 5 |
(2)P(ξ≥1)=P(ξ=1)+P(ξ=2)=0.095+0.002 5=0.097 5.


科目:高中数学 来源:2012年人教A版高中数学选修2-3 2.2二项分布及其应用练习卷(解析版) 题型:解答题
某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数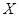 的概率分布
的概率分布
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com