Question

已知k是整数,钝角△ABC的三内角A、B、C所对的边分别为a、b、c.

(1)若方程组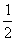有实数解,求k的值.

(2)对于(1)中k值,若sinC=,且有关系式(c-b)sin²A+bsin²B=csin²C,试求A、B、C的度数.

Answer 1

思路分析:由方程组有实解,求得k值,由已知关系式,讨论k的取值范围和角的取值.

解:(1)将原方程组消去y后,化为

x²-2kx+3k²-7k+3=0.

由Δ=4k²-4(3k²-7k+3)≥0,

得2k²-7k+3≤0,

即(k-3)(2k-1)≤0,解得≤k≤3.

∵k为整数,∴k=1,2,3.

(2)∵△ABC为钝角三角形,

∴0＜sinC＜1.

因此取k=1,得sinC=.

∴C=45°或135°.

由(c-b)sin²A+bsin²B=csin²C.

由正弦定理:a=2RsinA,b=2RsinB,c=2RsinC,得(c-b)·a²+b³-c³=0.

∴(c-b)(a²-c²-b²-bc)=0.

若c=b,则B=45°或135°,与△ABC是钝角三角形相矛盾.

∴a²-c²-b²-bc=0.

=-.∴cosA=-.

∴A=120°,C=45°,C=135°(舍去),

B=180°-120°-45°=15°.