[题目]在等腰梯形ABCD中.AB∥CD.且|AB|=2.|AD|=1.|CD|=2x其中x∈(0.1).以A.B为焦点且过点D的双曲线的离心率为e1 . 以C.D为焦点且过点A的椭圆的离心率为e2 . 若对任意x∈(0.1)不等式t＜e1+e2恒成立.则t的最大值为( )A.B.C.2D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x其中x∈（0，1），以A，B为焦点且过点D的双曲线的离心率为e1 ，以C，D为焦点且过点A的椭圆的离心率为e2 ，若对任意x∈（0，1）不等式t＜e1+e2恒成立，则t的最大值为（）
A.
B.
C.2
D.

【答案】B
【解析】解：在等腰梯形ABCD中，BD2=AD2+AB2﹣2ADABcos∠DAB =1+4﹣2×1×2×（1﹣x）=1+4x，
由双曲线的定义可得a1= ，c1=1，e1= ，
由椭圆的定义可得a2= ，c2=x，e2= ，
则e1+e2= + = + ，
令t= ∈（0， ﹣1），
则e1+e2= （t+ ）在（0， ﹣1）上单调递减，
所以e1+e2＞ ×（ ﹣1+ ）= ，
故选：B．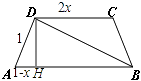

根据余弦定理表示出BD，进而根据双曲线的定义可得到a1的值，再由AB=2c1 ， e= 可表示出e1 ，同样的在椭圆中用c2和a2表示出e2 ，然后利用换元法即可求出e1+e2的取值范围，即得结论

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】下列函数：①f（x）=3|x| ， ②f（x）=x3 ， ③f（x）=ln ，④f（x）=x ，⑤f（x）=﹣x2+1中，既是偶函数，又是在区间（0，+∞）上单调递减函数为．（写出符合要求的所有函数的序号）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知直线l与椭圆交于两点A（x1 ， y1），B（x2 ， y2），椭圆上的点到下焦点距离的最大值、最小值分别为，向量 =（ax1 ， by1）， =（ax2 ， by2），且 ⊥ ，O为坐标原点．（Ⅰ）求椭圆的方程；
（Ⅱ）判断△AOB的面积是否为定值，如果是，请给予证明；如果不是，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=a x（a＞0且a≠1）的图象经过点（2，）
（1）求a的值
（2）比较f（2）与f（b2+2）的大小．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设全集U={1，2，3，4，5}，集合A={2，3，4}，B={2，5}，则B∪（UA）=（）
A.{5}
B.{1，2，5}
C.{1，2，3，4，5}
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则它的体积为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（Ⅰ）计算：2 ﹣（） +lg +（ ﹣1）lg1+（lg5）2+lg2lg50
（Ⅱ）已知x +x =3，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】经市场调查，东方百货超市的一种商品在过去的一个月内（以30天计算），销售价格f（t）与时间（天）的函数关系近似满足，销售量g（t）与时间（天）的函数关系近似满足g（t）= ．
（1）试写出该商品的日销售金额W（t）关于时间t（1≤t≤30，t∈N）的函数表达式；
（2）求该商品的日销售金额W（t）的最大值与最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数的定义域为集合，函数的定义域为集合 .
（1）若，求实数的取值范围；
（2）若，求实数的取值范围.

查看答案和解析>>

同步练习册答案