
分析 (I)设直线l的方程为my=x-4,与椭圆方程联立化为(3m2+4)y2+24my+36=0,△≥0,解得m2≥4.设A(x1,y1),B(x2,y2).由∠AOB为钝角(O为原点),可得$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2<0,把根与系数的关系代入即可得出.
(II)由(I)可得A1(x1,-y1),F(1,0).$\overrightarrow{F{A}_{1}}$=(x1-1,-y1),$\overrightarrow{FB}$=(x2-1,y2),利用向量共线定理即可判断出.
解答 解:(I)设直线l的方程为my=x-4,联立$\left\{\begin{array}{l}{my=x-4}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,
化为(3m2+4)y2+24my+36=0,
△=(24m)2-4(3m2+4)×36≥0,解得m2≥4.
设A(x1,y1),B(x2,y2).
则y1+y2=$\frac{-24m}{3{m}^{2}+4}$,y1y2=$\frac{36}{3{m}^{2}+4}$.
∵∠AOB为钝角(O为原点),
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2<0,化为(m2+1)y1y2+4m(y1+y2)+16<0.
∴$\frac{36({m}^{2}+1)}{3{m}^{2}+4}$-$\frac{96{m}^{2}}{3{m}^{2}+4}$+16<0,
化为3m2>25,
解得$-\frac{\sqrt{3}}{5}<\frac{1}{m}<\frac{\sqrt{3}}{5}$,且$\frac{1}{m}$≠0,
∴直线l的斜率的取值范围是$(-\frac{\sqrt{3}}{5},0)$∪$(0,\frac{\sqrt{3}}{5})$.
(II)由(I)可得A1(x1,-y1),F(1,0).
$\overrightarrow{F{A}_{1}}$=(x1-1,-y1),$\overrightarrow{FB}$=(x2-1,y2).
∴(x1-1)y2+y1(x2-1)=(my1+3)y2+y1(my2+3)=2my1y2+3(y1+y2)=$\frac{72m}{3{m}^{2}+4}-\frac{72m}{3{m}^{2}+4}$=0,
∴$\overrightarrow{F{A}_{1}}$∥$\overrightarrow{FB}$,即A1和F,B三点共线.
点评 本题考查了直线与椭圆相交问题、一元二次方程的根与系数的关系、向量夹角公式、数量积运算性质、向量共线定理,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
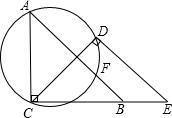 已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.
已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
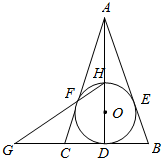 如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.
如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
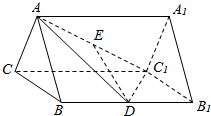 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
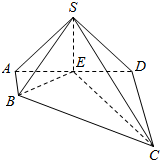 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
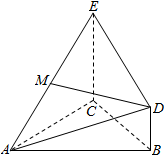 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
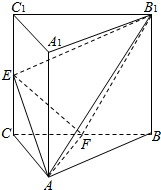 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com