解:(1)令x=-1,y=1,则
∵f(x+y)-f(y)=x(x+2y+1)
∴f(0)-f(1)=-1(-1+2+1)
∴f(0)=-2
(2)令y=0,则f(x)-f(0)=x(x+1)
又∵f(0)=-2
∴f(x)=x
2+x-2
(3)不等式f(x)+3<2x+a,即x
2+x-2+3<2x+a,即x
2-x+1<a,即

恒成立
当

时,
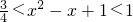
,故A={a|a≥1}
g(x)=x
2+x-2-ax=x
2+(1-a)x-2
∵g(x)在[-2,2]上是单调函数,
∴

或
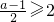
∴B={a|a≤-3,或a≥5}
∴A∩C
RB={a|1≤a<5}
分析:(1)令x=-1,y=1,利用f(x+y)-f(y)=x(x+2y+1),即可求得f(0)的值;
(2)令y=0,则f(x)-f(0)=x(x+1),结合f(0)=-2,可求f(x)的解析式;
(3)不等式f(x)+3<2x+a,即x
2+x-2+3<2x+a,即x
2-x+1<a,即

,根据

,可得
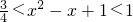
,从而可得A={a|a≥1},根据g(x)在[-2,2]上是单调函数,可求B={a|a≤-3,或a≥5},从而可求A∩C
RB.
点评:本题以抽象函数为载体,考查赋值法的运用,考查恒成立问题,解题的关键是利用二次函数的性质化简集合A,B.

 时,不等式f(x)+3<2x+a恒成立的实数a构成的集合记为A;又当x∈[-2,2]时,满足函数g(x)=f(x)-ax是单调函数的实数a构成的集合记为B,求A∩CRB(R为全集).
时,不等式f(x)+3<2x+a恒成立的实数a构成的集合记为A;又当x∈[-2,2]时,满足函数g(x)=f(x)-ax是单调函数的实数a构成的集合记为B,求A∩CRB(R为全集). 恒成立
恒成立 时,
时,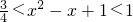 ,故A={a|a≥1}
,故A={a|a≥1} 或
或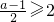
 ,根据
,根据 ,可得
,可得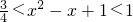 ,从而可得A={a|a≥1},根据g(x)在[-2,2]上是单调函数,可求B={a|a≤-3,或a≥5},从而可求A∩CRB.
,从而可得A={a|a≥1},根据g(x)在[-2,2]上是单调函数,可求B={a|a≤-3,或a≥5},从而可求A∩CRB.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案