Question

设x固定时，y为正态变量，对x、y有下表所示观察值：

x	－2.0	0.6	1.4	1.3	0.1	－1.6	－1.7	0.7	－1.8	－1.1
y	－6.1	－0.5	7.2	6.9	－0.2	－2.1	－3.9	3.8	－7.5	－2.1

（1）求y与x的线性回归方程；

（2）求相关系数，检验线性关系的显著性；

（3）若要求|y|＜4，x应控制在何范围内？

Answer 1

解：将数据列表如下：

序号	xi	yi	xi2	yi2	xiyi
1	－2.0	－6.1	4	37.21	12.2
2	0.6	－0.5	0.36	0.25	－0.30
3	1.4	7.2	1.96	51.84	10.08
4	1.3	6.9	1.69	47.61	8.97
5	0.1	－0.2	0.01	0.04	－0.02
6	－1.6	－2.1	2.56	4.41	3.36
7	－1.7	－3.9	2.89	15.21	6.63
8	0.7	3.8	2.49	14.44	2.66
9	－1.8	－7.5	3.24	56.26	13.5
10	－1.1	－2.1	1.21	4.41	2.31
∑	－4.1	－4.5	18.41	231.67	59.39

（1）由以上数据，可得

==－0.41，==－0.45，

b=3.44，a=0.96.

则线性回归方程为y=0.96+3.44x.

（2）由样本值，得

x_iy_i－10=59.39－10×（－0.41）×（－0.45）=57.545，

x_i²－10=18.41－10×（－0.41）²=16.729，

y_i²－10=231.67－10×（－0.45）²=229.645，

r==0.928.

对于a=0.01，自由度为8，查相关系数表得临界值r_0.01=0.765，因为r=0.928＞0.765=r_0.01，故知x与y的线性关系显著.

（3）当要求|y|＜4时，代入公式得

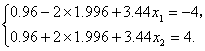
解之得x₁=－0.282，x₂=－0.277.故x的控制区间为（－0.282，－0.277）.