分析:根据动点P(x,y)满足条件|PF
1|+|PF
2|=a,当a<6,动点P的轨迹不存在,当a=6,动点P的轨迹为线段,当a>6,动点P的轨迹为椭圆,可分析①的真假;
根据点在抛物线开口外,则与抛物线交点只有一个的直线有3条,点在抛物线上,则与抛物线交点只有一个的直线有2条,点在抛物线开口内,则与抛物线交点只有一个的直线有1条,可分析②的真假;
根据离心率为
,长轴长为8,分焦点在x轴上和焦点在y轴上两种情况分别求出椭圆的标准方程,可判断③的真假;
根据3<k<4,可分析出二次曲线
+=1的图象形状及焦点位置,进而判断④的真假;
解答:解:①中,若a<6,则动点P的轨迹不存在,故①错误;
过点(0,1)作直线,使它与抛物线y
2=4x仅有一个公共点,这样的直线与抛物线相切(共有两条),或与对称轴平行(共有一条),共有3条,故②正确;
离心率为
,长轴长为8的椭圆标准方程为
+=1或
+=1,故③错误;
若3<k<4,则二次曲线
+=1为双曲线,则c
2=(4-k)+(k-3)=1,此时c=1,且焦点在x轴上,故焦点坐标是(±1,0),故④正确
故答案为:②④
点评:本题以命题的真假判断为载体考查了圆锥曲线的定义,性质及方程,熟练掌握圆锥曲线的定义,性质,标准方程是解答的关键.



 ,长轴长为8的椭圆标准方程为
,长轴长为8的椭圆标准方程为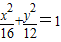 ;
;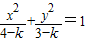 的焦点坐标是(±1,0).
的焦点坐标是(±1,0). ,长轴长为8的椭圆标准方程为
,长轴长为8的椭圆标准方程为 ;
; 的焦点坐标是(±1,0).
的焦点坐标是(±1,0). ,长轴长为8的椭圆标准方程为
,长轴长为8的椭圆标准方程为 ;
; 的焦点坐标是(±1,0).
的焦点坐标是(±1,0). ,长轴长为8的椭圆标准方程为
,长轴长为8的椭圆标准方程为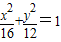 ;
;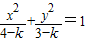 的焦点坐标是(±1,0).
的焦点坐标是(±1,0).