
若给定椭圆C:ax2+by2=1(a>0,b>0,a![]() b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,
b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,
(1)若N(x0,y0)在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
(2)命题:“若点N(x0,y0)在椭圆C的外部,则直线l与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
(3)若N(x0,y0)在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交l于M点(异于A、B),设![]() ,
,![]() ,问
,问![]() 是否为定值?说明理由.
是否为定值?说明理由.
(1)见解析(2)见解析(3) 见解析
(1)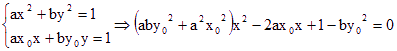
即ax2–2ax0x+ax02=0
∴△=4a2x02–4a2x02=0
∴l与椭圆C相切. (0.34)
(2)逆命题:若直线l:ax0x+by0y=1与椭圆C相交,则点N(x0,y0)在椭圆C的外部.
是真命题。联立方程得(aby02+a2x02)x2–2ax0x+1–by02=0
则△=4a2x02–4a(by02+ax02)(1–by02)>0
∴ax02–by02+b2y04–ax02+abx02y02>0
∴by02+ax02>1
∴N(x0,y0)在椭圆C的外部. (0.75)
(3)同理可得此时l与椭圆相离,设M(x1,y1),A(x,y)
则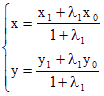 代入椭圆C:ax2+by2=1,利用M在l上,
代入椭圆C:ax2+by2=1,利用M在l上,
即ax0x1+by0y1=1,整理得(ax02+by02–1)![]() 12+ax12+by12–1=0
12+ax12+by12–1=0
同理得关于![]() 2的方程,类似.
2的方程,类似.
即![]() 1、
1、![]() 2是(ax02+by02–1)
2是(ax02+by02–1)![]() 2+ax12+by12–1=0的两根
2+ax12+by12–1=0的两根
∴


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| MA |
| AN |
| MB |
| BN |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| MA |
| AN |
| MB |
| BN |
查看答案和解析>>
科目:高中数学 来源:2008年上海市上海中学高三3月综合练习数学试卷1(文理合卷)(解析版) 题型:解答题
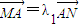 ,
,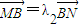 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.查看答案和解析>>
科目:高中数学 来源:2010年上海市上海中学高三数学综合练习试卷(1)(解析版) 题型:解答题
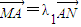 ,
,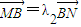 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com