
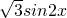 ,2cosx),x∈R.
,2cosx),x∈R. ,b+c=3(b>c),求b,c的值.
,b+c=3(b>c),求b,c的值. •
• =4cos2x+
=4cos2x+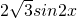 =2cos2x+2
=2cos2x+2 sin2x=
sin2x=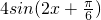 +2,
+2, ,有余弦定理cosA=
,有余弦定理cosA= =
=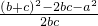 ,a=
,a= ,
, •
• ,然后利用二倍角的余弦函数公式化简,再提取4,利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域即可求出f(x)的最大值,根据周期公式T=
,然后利用二倍角的余弦函数公式化简,再提取4,利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域即可求出f(x)的最大值,根据周期公式T=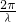 即可求出f(x)的最小正周期;
即可求出f(x)的最小正周期;

科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| 3 |
| n |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com