
分析 (1)移项,转化为解不等式组,求出解集即可;(2)求出x+y=1,根据基本不等式的性质求出代数式的最小值即可.
解答 解:(1)原不等式转化为:
$\left\{\begin{array}{l}{(x-1)(x-2)≥0}\\{x-2≠0}\end{array}\right.$,
解得x≤1或x>2,
∴原不等式的解集为{x|x≤1或x>2};
(2)∵x>0,y>0,x+y=1,
∴$\frac{4}{x}$+$\frac{9}{y}$=(x+y)($\frac{4}{x}$+$\frac{9}{y}$)=13+$\frac{4y}{x}$+$\frac{9x}{y}$
≥13+2$\sqrt{\frac{4y}{x}•\frac{9x}{y}}$=25,
当且仅当$\frac{4y}{x}$=$\frac{9x}{y}$时等号成立,
由$\left\{\begin{array}{l}x+y=1\\ \frac{4y}{x}=\frac{9x}{y}\end{array}$得$\left\{\begin{array}{l}x=\frac{2}{5}\\ y=\frac{3}{5}.\end{array}$
∴当x=$\frac{2}{5}$,y=$\frac{3}{5}$时取等号,
∴$\frac{4}{x}$+$\frac{9}{y}$的最小值为25.
点评 本题考查了解不等式问题,考查基本不等式的性质,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{16}{13}$ | C. | $\frac{32}{13}$ | D. | $\frac{30}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,∠A=∠B是sin∠A=sin∠B的充要条件 | |
| B. | 命题“若|x|>|y|,则x>y”的否命题是“若|x|≤|y|,则x≤y” | |
| C. | 复数(a+bi)(1+i)与复数-1+3i相等的充要条件是“a=1,b=2” | |
| D. | 命题“?x∈(0,+∞),2x>1”的否定是“?x0∈(-∞,0],2${\;}^{{x}_{0}}$≤1” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)是减函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a≥$\frac{8}{9}$ | C. | a≥$\frac{7}{8}$ | D. | a≥$\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
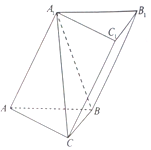 如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.
如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=0.4x+2.3 | B. | y=2x+2.4 | C. | y=-2x+9.5 | D. | y=-0.4x+4.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com