3

分析:由题意

,可知

,设出

与

的夹角,推出

与

的夹角,即可求出
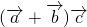
的表达式,通过三角变换,求出最大值.
解答:因为

,可知

,设

与

的夹角为α,
因为要求
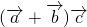
的最大值,所以

与

的夹角为
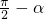
,
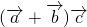
=
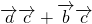
=
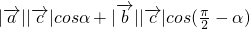
=3cosα+6sinα=3
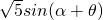
,其中tanθ=

,
所以
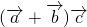
的最大值是:
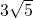
.
故答案为
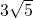
.
点评:本题是中档题,考查向量的数量积的应用,注意到不等式的最大值,确定向量间的夹角是解题的关键.注意辅助角公式的应用,考查计算能力.
练习册系列答案
相关习题
科目:高中数学
来源:2013-2014学年天津市蓟县高三上学期期中考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省高三上学期第三次月考文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2014届四川省绵阳市高二12月月考理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省高三模拟考试理科数学
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2010-2011学年江苏省泰州市高三第一次模拟考试数学卷
题型:填空题
查看答案和解析>>

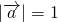 ,
,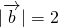 ,
, ,且
,且 ,则
,则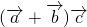 的最大值是________.
的最大值是________.