
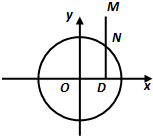
 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且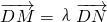 (λ>0).
(λ>0).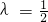 时,(1)所得曲线记为C,已知直线
时,(1)所得曲线记为C,已知直线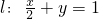 ,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.
,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.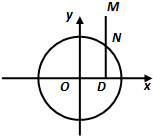 解:(1)设M(x,y),N(x0,y0),
解:(1)设M(x,y),N(x0,y0),
由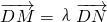 得 x=x0,y=λy0,
得 x=x0,y=λy0,
∴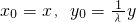
把N(x0,y0)代入圆的方程得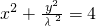 ,
,
化简得
当0<λ<1时,M的轨迹表示焦点在x轴上的椭圆
(2))当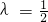 时,(1)所得曲线C为
时,(1)所得曲线C为 .
.
设P(x1,y1),R(x2,y2),Q(x,y)
∵P在l上、R在椭圆上,∴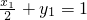 ①
①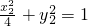 ②
②
设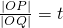 ,由比例性质得
,由比例性质得 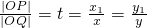 ,∴x1=tx,y1=ty
,∴x1=tx,y1=ty
代入①得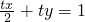 ③
③
∵|OQ|•|OP|=|OR|2,∴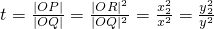 ,
,
∴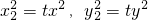
代入②得 ④
④
由③④联立得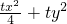 =
=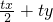 ,又t≠0,
,又t≠0,
∴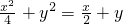 ,原点除外.
,原点除外.
化简得点Q的轨迹方程为x2-2x+4y2-4y=0(原点除外).
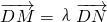 ,确定动点坐标之间的关系,利用点N在圆x2+y2=4上运动,可以得到点M的轨迹方程,从而可得λ为何值时M的轨迹表示焦点在x轴上的椭圆;
,确定动点坐标之间的关系,利用点N在圆x2+y2=4上运动,可以得到点M的轨迹方程,从而可得λ为何值时M的轨迹表示焦点在x轴上的椭圆;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图所示,已知圆C:(x+1)2+y2=8,顶点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,顶点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且| DM |
| DN |
| 1 |
| 2 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源:0119 期中题 题型:解答题
 (λ>0),
(λ>0), 时,(1)所得曲线记为C,已知直线l:
时,(1)所得曲线记为C,已知直线l: +y=1,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,求点Q的轨迹方程。
+y=1,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,求点Q的轨迹方程。 
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省广州市实验中学高二(上)期中数学试卷(解析版) 题型:解答题
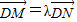 (λ>0).
(λ>0).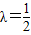 时,(1)所得曲线记为C,已知直线
时,(1)所得曲线记为C,已知直线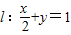 ,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.
,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.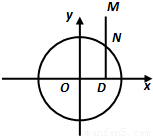
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com