
(1)平面内有9个点,其中4个点在一条直线上,此外没有3个点在一条直线上,过这9个点可以作_________个三角形;
(2)空间12个点,其中5个点共面,此外无任何4个点共面,这12个点可决定________个不同的平面.
思路解析:根据能否构成三角形(平面)把点分类.
(1)从第二类中任意选取三个点,可作![]() 个三角形;
个三角形;
从第一类中任意选取1个点,从第二类中任意选取2个点,可作![]() 个三角形;
个三角形;
从第一类中任意选取2个点,从第二类中任意选取1个点,可作![]() 个三角形;
个三角形;
利用分类计数原理,总共可作三角形的个数为![]() =80(个).
=80(个).
注意:本题也可解为![]() =80(个),请同学们加以解释.
=80(个),请同学们加以解释.
(2)这个问题可分四类加以考虑.
①5个共面点决定1个平面;
②5个共面点中任何2个点和其余7个点中任意一点决定![]() 个平面;
个平面;
③5个共面点中任一点和其余7个点中任意2个点决定![]() 个平面;
个平面;
④7个点中任何3个点决定![]() 个平面.
个平面.
总共决定平面的个数为1+![]() +
+![]() +
+![]() =211.
=211.
答案:(1)80 (2)211


科目:高中数学 来源: 题型:
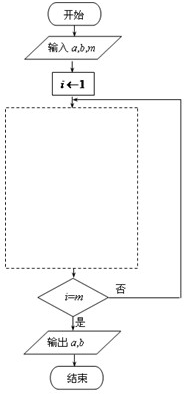 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,
|
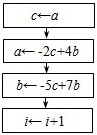 B、
B、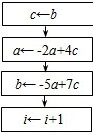
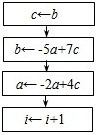 D、
D、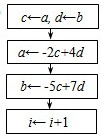
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
完成下列各填空题.
(1)平面内有9个点,其中4个点在一条直线上,此外没有3个点在一条直线上,过这9个点可以作_________个三角形;
(2)空间12个点,其中5个点共面,此外无任何4个点共面,这12个点可决定________个不同的平面.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com