
(06年重庆卷理)(13分)
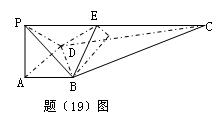
如图,在四棱锥![]() 中,
中,![]() 底面ABCD,
底面ABCD,![]() 为直角,
为直角,![]() ,
,![]() E、F分别为
E、F分别为![]() 、
、![]() 中点。
中点。
(I)试证:![]() 平面
平面![]() ;
;
(II)高![]() ,且二面角
,且二面角 ![]() 的平面角大小
的平面角大小![]() ,求
,求![]() 的取值范围。
的取值范围。
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
(06年重庆卷理)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg),得到频率分布直方图如下:
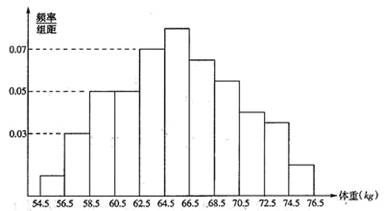
根据上图可得这100名学生中体重在![]() 的学生人数是( )
的学生人数是( )
(A)20 (B)30 (C)40 (D)50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com