
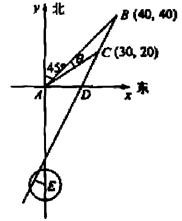
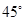 且与点A相距40
且与点A相距40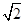 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东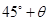 (其中
(其中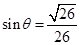 ,
,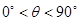 )且与点A相距10
)且与点A相距10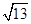 海里的位置C.
海里的位置C. 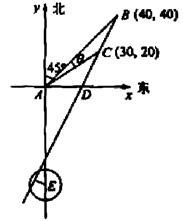
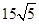 海里/小时;(2)船会进入警戒水域
海里/小时;(2)船会进入警戒水域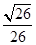 ,求出θ的余弦值,再由余弦定理求出BC的值,从而可得到船的行驶速度.
,求出θ的余弦值,再由余弦定理求出BC的值,从而可得到船的行驶速度.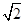 ,AC=10
,AC=10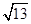 ,
,
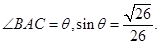 ………2分
………2分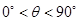 ,所以cos
,所以cos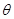 =
=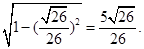 ………4分
………4分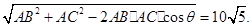 ……6分
……6分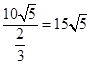 (海里/小时) ………7分
(海里/小时) ………7分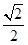 AB=40, ………8分
AB=40, ………8分 ,
,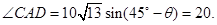 ………10分
………10分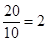 ,直线l的方程为y=2x-40. ………11分
,直线l的方程为y=2x-40. ………11分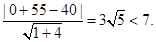 ………13分
………13分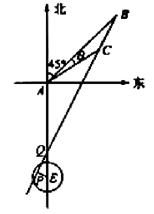
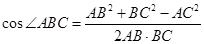
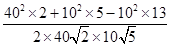 =
=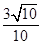 .
.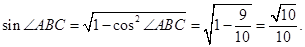
 中,由正弦定理得,
中,由正弦定理得,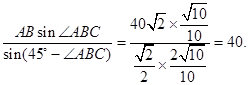
 BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.
 中,PE=QE·sin
中,PE=QE·sin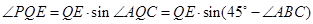
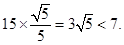 所以船会进入警戒水域.
所以船会进入警戒水域.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com