
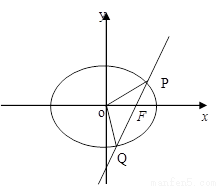
已知直线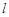 过椭圆E:
过椭圆E: 的右焦点
的右焦点 ,且与E相交于
,且与E相交于 两点.
两点.
(1)设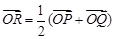 (
(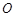 为原点),求点
为原点),求点 的轨迹方程;
的轨迹方程;
(2)若直线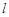 的倾斜角为
的倾斜角为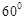 ,求
,求 的值.
的值.
(1)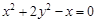 ;(2)
;(2)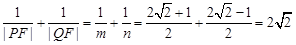
【解析】第一问中,利用向量的表达式,坐标的手段得到所求点的轨迹方程。
当直线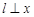 轴时,直线
轴时,直线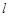 的方程是:
的方程是: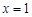 ,根据对称性可知
,根据对称性可知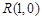
当直线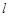 的斜率存在时,可设直线
的斜率存在时,可设直线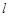 的方程为
的方程为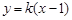
代入E有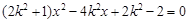
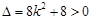 ;
; 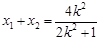
第二问中,在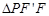 中
中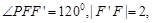 设
设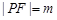 ,则
,则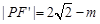
由余弦定理得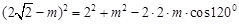
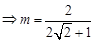
同理,在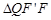 ,设
,设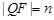 ,则
,则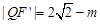
也由余弦定理得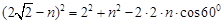
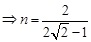
然后可得。
解:(1)设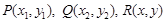
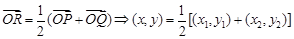
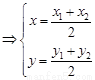
由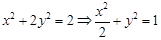 ,易得右焦点
,易得右焦点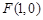 -(2分)
-(2分)
当直线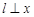 轴时,直线
轴时,直线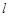 的方程是:
的方程是: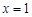 ,根据对称性可知
,根据对称性可知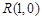
当直线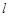 的斜率存在时,可设直线
的斜率存在时,可设直线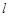 的方程为
的方程为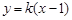
代入E有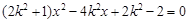
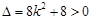 ;
; 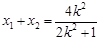 ---(5分)
---(5分)
于是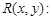
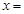
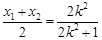 ;
; 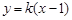
消去参数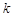 得
得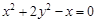 而
而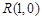 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是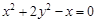 ----(8分)
----(8分)
(2)设椭圆另一个焦点为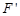 ,
,
在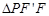 中
中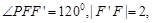 设
设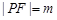 ,则
,则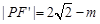
由余弦定理得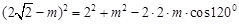
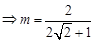
同理,在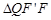 ,设
,设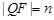 ,则
,则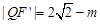
也由余弦定理得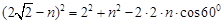
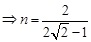
于是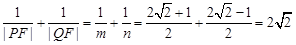 ………12分
………12分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com