
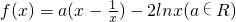 .
. )-
)- =
=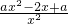 ,…(1分)
,…(1分)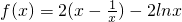 ,
, )-
)- .
.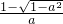 或x>
或x>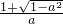 ;…(8分)
;…(8分)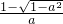 <x<
<x<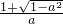 .…(9分)
.…(9分)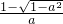 )和(
)和(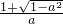 ,+∞),
,+∞),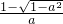 ,
,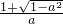 ). …(11分)
). …(11分)

科目:高中数学 来源: 题型:
(08年银川一中二模文) (12分)已知函数![]() .
.
(1)若a,b都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率.
(2)若a,b都是从区间[0,4]任取的一个数,求f(1)>0成立时的概率.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南通市西亭高级中学高三(上)期中数学复习试卷(五)(解析版) 题型:解答题
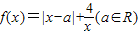 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南通市西亭高级中学高三(上)期中数学复习试卷(五)(解析版) 题型:解答题
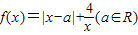 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区示范校高三(下)3月联考数学试卷(文科)(解析版) 题型:解答题
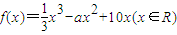 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com