
分析 (1)根据函数奇偶性的定义和性质进行求解即可.
(2)根据不等式求出a的取值范围,判断函数的单调性,将不等式恒成立进行转化即可.
(3)利用换元法,结合一元二次函数单调性的性质进行求解即可.
解答 解:(1)∵f(x)是定义域为R的奇函数,∴f(0)=0,
∴1-(k-1)=0,∴k=2,…(2分)
(2)f(x)=ax-a-x(a>0且a≠1),
若f(1)<0,则a-$\frac{1}{a}$<0,
∵a>0且a≠1,
∴a2-1<0,即0<a<1 …(4分)
∵ax单调递减,a-x单调递增,
故f(x)在R上单调递减.
不等式化为f(x2+tx)<f(x-4),
∴x2+tx>x-4,即x2+(t-1)x+4>0恒成立
∴△=(t-1)2-16<0,解得-3<t<5
$(3)∵f(1)=\frac{3}{2}$…(8分),
∴$a-\frac{1}{a}=\frac{3}{2},即2{a^2}-3a-2=0$,
∴$a=2或a=-\frac{1}{2}(舍去)$…(9分)
g(x)=22x+2-2x-2(2x-2-x)=(2x-2-x)2-2(2x-2-x)+2
令t=2x-2-x
∵t=2x-2-x在[1,+∞)上为递增的,
∴$t∈[\frac{3}{2},+∞)$…(12分)
∴设h(t)=t2-2t+2=(t-1)2+1,$t∈[\frac{3}{2},+∞)$
∴$h{(t)_{min}}=h(\frac{3}{2})=\frac{5}{4}$,
即g(x)在[1,+∞)上的最小值为$\frac{5}{4}$.…(14分)
点评 本题主要考查函数恒成立问题,利用换元法结合一元二次函数的性质是解决本题的关键.综合较强.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤1} | C. | {x|x<-2} | D. | {x|x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
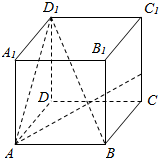 在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.
在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com