分析:(1)设焦距为2a,c>0,由点(c,0)到y=-x-c距离为
=,得c=1.左准线
x=-=-a2,设A(x
1,y
1),B(x
2,y
2),则
x1+a2+x2+a2=,由
,得(a
2+b
2)x
2+2a
2cx+a
2c
2-a
2b
2=0,由此能求出椭圆的方程.
(2)设l:y=k(x+1),k≠0,由
,得(2k
2+1)x
2+4k
2x
2+2k
2-2=0,故
x1+x2=-,
x1x2=,△=8(k
2+1)>0,所以
|AB|=|x1-x2|=2
•.点O到AB距离为
d=,由此能求出△AOB面积的最大值.
解答:解:(1)设焦距为2a,c>0,由点(c,0)到y=-x-c距离为
=,得c=1.
故左准线
x=-=-a2,
设A(x
1,y
1),B(x
2,y
2),
则
x1+a2+x2+a2=,
由
,
得(a
2+b
2)x
2+2a
2cx+a
2c
2-a
2b
2=0,
∴
x1+x2=-=-,
∴
2a2-=,
∴a
2=2,
∴椭圆的方程为:
+y2=1.
(2)设l:y=k(x+1),k≠0,
由
,得(2k
2+1)x
2+4k
2x
2+2k
2-2=0,
∵
x1+x2=-,
x1x2=,△=8(k
2+1)>0,
∴
|AB|=|x1-x2|=
•=2
•.
点O到AB距离为
d=,
∵△AOB面积
S=|AB|•d=
•,
∴
S<•=
,
当l:x=-1时,
S=××1=,
故在l:x=-1时△AOB面积的最大值为
.
点评:本题考查椭圆的方程的求法和求△AOB面积的最大值.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.



 ,
, ,
, .
.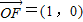 ,
, ,
, .
. ,
,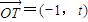 ,
, .
.