练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知以点A(-1,2)为圆心的圆与直线：相切.

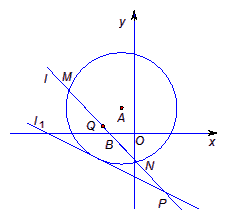    过点B(-2,0)的动直线与圆A相交与、两点，是的中点，直线与相交于点.

    (I) 求圆A的方程；

    （II）当时，求直线的方程；

    （III）是否为定值，如果是，求出定值；如果不是，请说明理由.

    同下


    解析:

    设圆A的半径为,由于圆A与直线：相切，

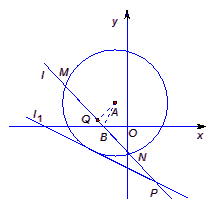
    ……………………………………………………….2分

    圆A的方程为……………………………………….4分

    (II) ①当直线与轴垂直时, 易知符合题意……………5分

    ②当直线与轴不垂直时,

    设直线的方程为，即，

    连结,则

    ∵，∴，………………………………………6分

    则由，得, ∴直线：.

    故直线的方程为或………………………………………9分

    (III)∵,∴ …10分

    当与轴垂直时，易得，则,又,

    ∴………………………………………………………11分

    ②当的斜率存在时，设直线的方程为，

    则由，得（）,则

    ∴

    综上所述，是定值，且.…………………14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交与M、N两点，Q是MN的中点，直线l与l1相交于点P．
    （I）求圆A的方程；
    （Ⅱ）当MN=2
    		19
    时，求直线l的方程；
    （Ⅲ）
    BQ
    •
    BP
    是否为定值，如果是，求出定值；如果不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l1相交于点P．
    （1）求圆A的方程；
    （2）当|MN|=2
    		19
    时，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知经过点A（-2，0），且以（λ，1+λ）为方向向量的直线l1与经过点B（2，0），且以（1+λ，-3λ）为方向向量的直线l2相交于点P，其中λ∈R．
    （1）求点P的轨迹C的方程；
    （2）是否存在直线l：y=kx+m（m≠0）与轨迹C相交于不同的两点M、N，且满足|BM|=|BN|？若存在，求出m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三点A（-2-a,0）,P(-2-a,t),F(a,0),其中a为大于零的常数，t为变数，平面内动点M满足·=0，且||=||+2.

    （1）求动点M的轨迹;

    （2）若动点M的轨迹在x轴上方的部分与圆心在C(a+4,0),半径为4的圆相交于两点S、T，求证：C落在以S、T为焦点过F的椭圆上.

    查看答案和解析>>

    同步练习册答案