
(1)求证:对m∈R,直线l与圆C总有两个不同的交点;
(2)设l与圆C交于A、B两点,若|AB|=![]() ,求l的倾斜角;
,求l的倾斜角;
(3)求弦AB的中点M的轨迹方程;
(4)若定点P(1,1)分弦AB为![]() =
=![]() ,求此时直线l的方程.
,求此时直线l的方程.
(1)证明:由已知l:y-1=m(x-1),
∴直线l恒过定点P(1,1).
∵12+(1-1)2=1<5,
∴P在圆C内.则直线l与圆C总有两个不同的交点.
(2)解:将直线l与圆C的方程联立,消去y得(1+m2)x2-2m2x+m2-5=0. (*)
设A(x1,y1)、B(x2,y2),则x1、x2为方程(*)的两实根,
∵|AB|=![]() |x1-x2|,
|x1-x2|,
∴![]() =
=![]() ·
·![]() .∴m2=3,m=±
.∴m2=3,m=±![]() .
.
∴l的倾斜角为α=![]() 或
或![]() .
.
(3)解:设M的坐标为(x,y),连结CM、CP,
∵C(0,1),P(1,1),|CM|2+|PM|2=|CP|2,∴x2+(y-1)2+(x-1)2+(y-1)2=1.
整理得轨迹方程为x2+y2-x-2y+1=0(x≠1).
(4)解:∵![]() =
=![]() ,
,
∴1=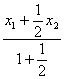 .∴
.∴![]() x1=
x1=![]() -
-![]() (x1+x2).
(x1+x2).
又∵x1+x2=![]() ,∴
,∴![]() x1=
x1=![]() ,x1=
,x1=![]() .
.
解方程(1+m2)x2-2m2x+m2-5=0,得x1=![]() ,
,
∴![]()
=![]() ,
,
解得m=±1.
∴直线l的方程为x-y=0或x+y-2=0.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2014届福建省福州市高一下学期期中数学试卷(解析版) 题型:填空题
已知圆C:x2+y2+2x+ay-3=0(a为实数)上任意一点关于直线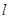 :x-y+2=0的对称点都在圆C上,则a=
.
:x-y+2=0的对称点都在圆C上,则a=
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com