练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，在两个底面对应边的比是1∶2的三棱台ABC—A1B1C1中，BB1∥截面A1EDC1，求截面A1EDC1截棱台ABC—A1B1C1成两部分体积之比.

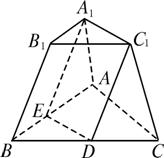
    解析：设三棱台的上、下底面的面积分别为S1和S2，高为h.

    ∵,∴,∴S2=4S1.

    ∴

    .

    ∵BB1∥截面A1EDC1，BB1侧面BCC1B1，且侧面BCC1B1与截面交于C1D，∴BB1∥C1D.同理可证BB1∥A1E，∴C1D∥A1E.

    ∵两底面互相平行，∴A1C1∥DE.

    ∴截面A1EDC1是平行四边形，∴A1C1=DE.

    同样可以证明B1C1=BD，A1B1=BE，

    即△A1B1C1≌△BDE.

    ∴多面体BDE-B1C1A1是棱柱，且.

    ∵三棱柱BDE-B1C1A1的高等于三棱台ABC-A1B1C1的高，等于h.

    ∴.

    ∴三棱台被截面A1EDC1截得的另一部分的体积等于

    .

    ∴截面A1EDC1截三棱台成两部分的体积之比为4∶3.

    点评：本题以棱台为载体，讨论直线与平面、平面与平面的平行关系，其关键是证明多面体BDE-B1C1A1为棱柱.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，在三棱柱A1B1C1-ABC中，AA1⊥底面ABC，AC⊥BC．AC=BC=CC1=2．
    （1）若点D、E、F分别为棱CC1、C1B1、CA的中点，求证：EF⊥平面A1BD；
    （2）请根据下列要求设计切割和拼接方法：要求用平行于三棱柱A1B1C1-ABC的某一条侧棱的平面去截此三棱柱，切开后的两个几何体再拼接成一个长方体．简单地写出一种切割和拼接方法，
    并写出拼接后的长方体的表面积（不必写出计算过程）．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年上海交大附中高三数学理总复习二空间向量与立体几何练习卷（解析版） 题型：解答题

    如图所示，在多面体ABCD－A1B1C1D1中，上、下两个底面A1B1C1D1和ABCD互相平行，且都是正方形，DD1⊥底面ABCD，AB∥A1B1，AB＝2A1B1＝2DD1＝2a.

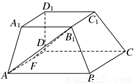
    (1)求异面直线AB1与DD1所成角的余弦值；

    (2)已知F是AD的中点，求证：FB1⊥平面BCC1B1.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图所示，在三棱柱A1B1C1-ABC中，AA1⊥底面ABC，AC⊥BC．AC=BC=CC1=2．
    （1）若点D、E、F分别为棱CC1、C1B1、CA的中点，求证：EF⊥平面A1BD；
    （2）请根据下列要求设计切割和拼接方法：要求用平行于三棱柱A1B1C1-ABC的某一条侧棱的平面去截此三棱柱，切开后的两个几何体再拼接成一个长方体．简单地写出一种切割和拼接方法，
    并写出拼接后的长方体的表面积（不必写出计算过程）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    解析：A错误．如图①所示，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不是棱锥．B错误．如答图②③所示，若△ABC不是直角三角形，或是直角三角形但旋转轴不是直角边，所得的几何体都不是圆锥．C错误．若六棱锥的所有棱都相等，则底面多边形是正六边形．由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长．D正确．

    答案：D

    查看答案和解析>>

    科目：高中数学 来源：2008年广东省广州市高二数学竞赛试卷（解析版） 题型：解答题

    如图所示，在三棱柱A1B1C1-ABC中，AA1⊥底面ABC，AC⊥BC．AC=BC=CC1=2．
    （1）若点D、E、F分别为棱CC1、C1B1、CA的中点，求证：EF⊥平面A1BD；
    （2）请根据下列要求设计切割和拼接方法：要求用平行于三棱柱A1B1C1-ABC的某一条侧棱的平面去截此三棱柱，切开后的两个几何体再拼接成一个长方体．简单地写出一种切割和拼接方法，
    并写出拼接后的长方体的表面积（不必写出计算过程）．

    查看答案和解析>>

    同步练习册答案