
已知函数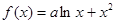 (
(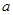 为实常数) .
为实常数) .
(1)当 时,求函数
时,求函数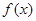 在
在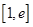 上的最大值及相应的
上的最大值及相应的 值;
值;
(2)当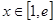 时,讨论方程
时,讨论方程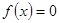 根的个数.
根的个数.
(3)若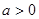 ,且对任意的
,且对任意的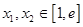 ,都有
,都有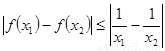 ,求实数a的取值范围.
,求实数a的取值范围.
(1)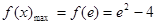 .
.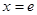 ;(2)
;(2)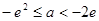 时,方程
时,方程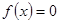 有2个相异的根.
有2个相异的根. 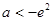 或
或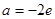 时,方程
时,方程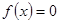 有1个根.
有1个根. 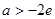 时,方程
时,方程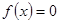 有0个根.(3)
有0个根.(3) .
.
【解析】
试题分析:(1)通过求导数可得函数的单调性,在对比区间的两端点的函数值即可求得函数的最大值.(2)由于参数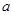 的变化.可以采取分离变量的方法,转化为两个函数的交点个数问题.其中一个是垂直于y轴的直线,另一个是通过求出函数的走向.根据图像即可得到结论.(3)将要说明的结论通过变形得到一个等价问题从而证明新的函数的单调性,使得问题巧妙地转化.本题只是容量大.通过研究函数的单调性,含参函数的讨论.与不等式的相结合转化为函数的单调性的证明.
的变化.可以采取分离变量的方法,转化为两个函数的交点个数问题.其中一个是垂直于y轴的直线,另一个是通过求出函数的走向.根据图像即可得到结论.(3)将要说明的结论通过变形得到一个等价问题从而证明新的函数的单调性,使得问题巧妙地转化.本题只是容量大.通过研究函数的单调性,含参函数的讨论.与不等式的相结合转化为函数的单调性的证明.
试题解析:(1)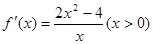 ,当
,当 时,
时,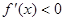 .当
.当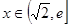 时,
时,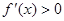 ,又
,又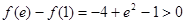 ,
,
故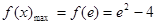 ,当
,当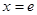 时,取等号
4分
时,取等号
4分
(2)易知 ,故
,故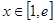 ,方程
,方程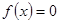 根的个数等价于
根的个数等价于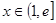 时,方程
时,方程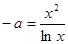 根的个数. 设
根的个数. 设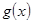 =
=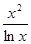 ,
,
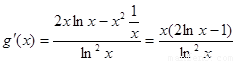
当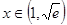 时,
时,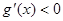 ,函数
,函数 递减,当
递减,当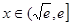 时,
时,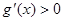 ,函数
,函数 递增.又
递增.又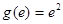 ,
,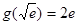 ,作出
,作出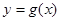 与直线
与直线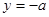 的图像,由图像知:
的图像,由图像知:
当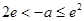 时,即
时,即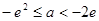 时,方程
时,方程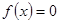 有2个相异的根;
有2个相异的根;
当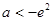 或
或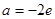 时,方程
时,方程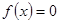 有1个根;
有1个根;
当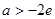 时,方程
时,方程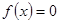 有0个根;
10分
有0个根;
10分
(3)当 时,
时,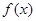 在
在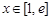 时是增函数,又函数
时是增函数,又函数 是减函数,不妨设
是减函数,不妨设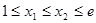 ,则
,则 等价于
等价于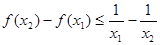
即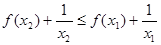 ,故原题等价于函数
,故原题等价于函数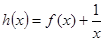 在
在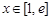 时是减函数,
时是减函数,
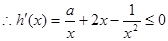 恒成立,即
恒成立,即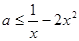 在
在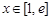 时恒成立.
时恒成立.
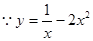 在
在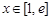 时是减函数
时是减函数  16分
16分
(其他解法酌情给分)
考点:1.函数的最值问题.2.函数的单调性.3.函数与不等式的关系以及转化为函数的单调性的证明.


科目:高中数学 来源:2013-2014学年上海市嘉定区高三上学期期末考试(一模)理科数学试卷(解析版) 题型:解答题
已知函数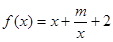 (
(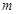 为实常数).
为实常数).
(1)若函数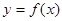 图像上动点
图像上动点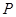 到定点
到定点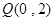 的距离的最小值为
的距离的最小值为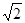 ,求实数
,求实数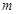 的值;
的值;
(2)若函数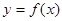 在区间
在区间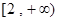 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数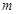 的取值范围;
的取值范围;
(3)设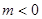 ,若不等式
,若不等式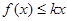 在
在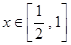 有解,求
有解,求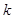 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年江西省高二第二学期期中考试理科数学 题型:解答题
(本大题共14分)
已知函数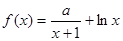 (
(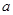 为实常数)的两个极值点为
为实常数)的两个极值点为 ,且满足
,且满足
(1)求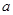 的取值范围;
的取值范围;
(2)比较 与
与 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com