已知方程①:ax2+bx+c=0,(其中c≠0)有整数根,是否存在整数P,使得方程②:x3+(x+P)x2+(b+P)x+c=0与方程①有相同的整数根?如果这样的P存在,请求出所有这样的整数P和相应的公共整数根;如果这样的P不存在,请说明你的理由.
解:x
3+(a+P)x
2+(b+P)x+c=0
则x
3+Px
2+Px+ax
2+bx+c=0而ax
2+bx+c=0
∴x
3+Px
2+Px=0则方程必有一个根为0,而ax
2+bx+c=0,(其中c≠0)无0根
∴x
2+Px+P=0与ax
2+bx+c=0有相同的整数根
而方程x
2+Px+P=0的根为
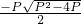
,要使
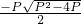
为整数,则
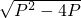
为整数
从而P=0或4,而P=0时方程x
3+(a+P)x
2+(b+P)x+c=0的根为0,而ax
2+bx+c=0,(其中c≠0)无0根,不合题意
∴P=4,此时方程x
2+Px+P=0的根为-2
分析:先根据已知条件将原题转化成x
2+Px+P=0与ax
2+bx+c=0有相同的整数根,然后利用求根公式求出方程x
2+Px+P=0的根,根据
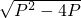
为整数则P=0或4,讨论可求出满足条件的P,从而求出公共整数根.
点评:本题主要考查了函数与方程的综合运用,以及整数解问题,同时考查了分析问题和解决问题的能力,属于中档题.

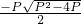 ,要使
,要使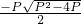 为整数,则
为整数,则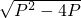 为整数
为整数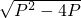 为整数则P=0或4,讨论可求出满足条件的P,从而求出公共整数根.
为整数则P=0或4,讨论可求出满足条件的P,从而求出公共整数根.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案