解:(Ⅰ)若
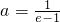
,则
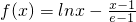
,
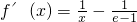
.
当x∈(0,e-1)时,f'(x)>0,f(x)单调递增;
当x∈(e-1,+∞)时,f'(x)<0,f(x)单调递减.…(2分)
又因为f(1)=0,f(e)=0,所以
当x∈(0,1)时,f(x)<0;当x∈(1,e-1)时,f(x)>0;
当x∈(e-1,e)时,f(x)>0;当x∈(e,+∞)时,f(x)<0.…(4分)
故y=|f(x)|的极小值点为1和e,极大值点为e-1.…(6分)
(Ⅱ)不等式
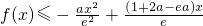
,
整理为
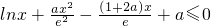
.…(*)
设
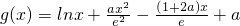
,
则
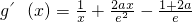
(x>0)=
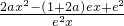
=
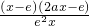
.…(8分)
①当a≤0时,2ax-e<0,又x>0,所以,
当x∈(0,e)时,g'(x)>0,g(x)递增;
当x∈(e,+∞)时,g'(x)<0,g(x)递减.
从而g(x)
max=g(e)=0.
故,g(x)≤0恒成立.…(11分)
②当a>0时,
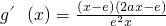
=
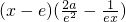
.
令
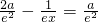
,解得
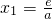
,则当x>x
1时,
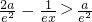
;
再令
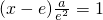
,解得
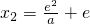
,则当x>x
2时,
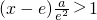
.
取x
0=max(x
1,x
2),则当x>x
0时,g'(x)>1.
所以,当x∈(x
0,+∞)时,g(x)-g(x
0)>x-x
0,即g(x)>x-x
0+g(x
0).
这与“g(x)≤0恒成立”矛盾.
综上所述,a≤0.…(14分)
分析:(Ⅰ)把
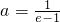
代入可得函数的解析式,进而可得导函数和单调区间,可得函数的极值点;
(Ⅱ)原不等式等价于
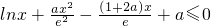
,设
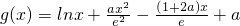
,通过求导数,分a≤0,和a>0讨论可得答案.
点评:本题考查利用导数研究函数的极值,涉及函数的恒成立问题,属中档题.

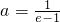 ,求函数y=|f(x)|的极值点;
,求函数y=|f(x)|的极值点;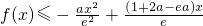 恒成立,求a的取值范围.
恒成立,求a的取值范围.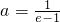 ,则
,则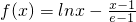 ,
,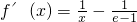 .
.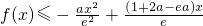 ,
,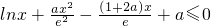 .…(*)
.…(*)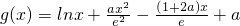 ,
,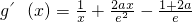 (x>0)=
(x>0)=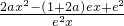 =
=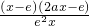 .…(8分)
.…(8分)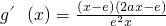 =
=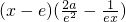 .
.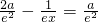 ,解得
,解得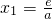 ,则当x>x1时,
,则当x>x1时,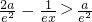 ;
;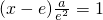 ,解得
,解得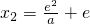 ,则当x>x2时,
,则当x>x2时,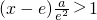 .
.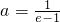 代入可得函数的解析式,进而可得导函数和单调区间,可得函数的极值点;
代入可得函数的解析式,进而可得导函数和单调区间,可得函数的极值点;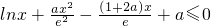 ,设
,设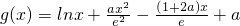 ,通过求导数,分a≤0,和a>0讨论可得答案.
,通过求导数,分a≤0,和a>0讨论可得答案.
