练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设集合M={x|x≤4}，又a=2．那么（　　）
    A、a⊆MB、a∉M
    C、{a}∈MD、{a}⊆M
    考点：集合的包含关系判断及应用
    专题：计算题,集合
    分析：由已知中集合M={x|x≤4}，a=2，我们易判断出元素a与集合M的关系，及集合{a}与集合M的关系，进而得到答案．
    解答： 解：∵M={x|x≤4}，a=2，
    ∴a∈M
    即{a}⊆M
    故选D．
    点评：本题考查的知识点是元素与集合关系的判断，集合与集合关系的判断，熟练掌握元素与集合关系的定义及集合与集合关系的定义，是解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

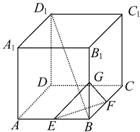    在棱长为1的正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹的长度为（　　）
    A、
    1
    2
    B、
    		2
    2
    C、
    		3
    3
    D、
    2
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直三棱柱ABC-A1B1C1的六个顶点在球O上，若AB=3，AC=4，AB⊥AC，AA1=12，则球O的面积为（　　）
    A、153πB、169π
    C、10πD、90π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y满足约束条件
    x+y≤1
    y≥-1
    x≥0
    ，则z=2x+y的最大值为
     
    ，最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数a≠0，函数f（x）=
    2x+a(x＜1)
    -x-2a(x≥1)
    ，若f（1-a）=f（1+a），则a的取值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，l1l2是通过某市开发区中心O的南北和东西走向的两条道路，连接M，N两地的铁路是一段抛物线弧，它所在的抛物线关于直线l1对称，M到l1，l2的距离分别是2km，4km；N到l1，l2的距离分别是3km，9km．该市拟在点O的正北方向建设一座工厂，要求厂址到点O的距离大于5km，而不超过8km，并且铁路上任意一点到工厂的距离不能小于
    		6
    km．则该厂离点O的最近距离为（工厂视为一点）（　　）
    A、6kmB、6.5km
    C、6.25kmD、7km

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    增城石滩某菜民想用篱笆围成一个的矩形菜园，请你设计此个矩形的长和宽，满足他下列要求：
    （1）用篱笆围成一个面积为100m2的矩形菜园，要所用篱笆最短；
    （2）一段长为36m的篱笆围成一个矩形菜园，菜园的面积最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=a1-x+1（a＞0，a≠1）的图象必经过的点是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在下列给出的四个命题中，为真命题的是（　　）
    A、?a∈R，?b∈Q，a2+b2=0
    B、?n∈Z，?m∈Z，nm=m
    C、?n∈Z，?m∈Z，n＞m2
    D、?a∈R，?b∈Q，a2+b2=1

    查看答案和解析>>

    同步练习册答案