解:(1)由
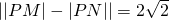
,知点P的轨迹是以M(-2,0),N(2,0)为焦点,
实轴长为

的双曲线.
即设
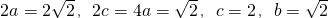
所以所求的W的方程为x
2-y
2=2
(2)若k不存在,即x=2时,可得A(2,

),B(2,-

),|AB|=2

满足题意;
若k存在,可设l:y=k(x-2)
联立
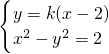
,?(1-k
2)x
2+4k
2x-4k
2-2=0
由题意知
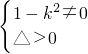
?k∈R且k≠±1
设A(x
1,y
1),B(x
2,y
2),则|AB|=
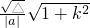
即
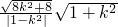
=2

?k=0即l:y=0
所以直线l的方程为x=2或y=0
(3)
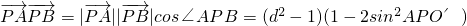
=
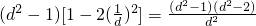
=
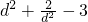
由
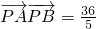
知5d
4-51d
2+10=0
∴
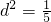
或10
设P(x,y),则d
2=x
2+(y-4)
2=y
2+2+(y-4)
2=2y
2-8y+18
所以
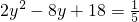
或2y
2-8y+18=10
解得y=2此时x=
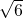
即P(
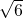
,2)
分析:(1)根据所给的动点P所满足的条件,看出点P是到两个定点距离之差等于定值,得到图形是双曲线,根据双曲线的定义,写出方程.
(2)本题是一个弦长问题,已知直线过定点,要设直线的方程,首先注意直线的斜率是否存在,不存在的情况要单独说明,存在时设出斜率,写出方程,联立方程,根据根和系数的关系,写出弦长的表达式,得到未知数.
(3)首先写出两个向量的数量积的表示式,用d来表示,根据数量积的值,得到关于d的方程,解出结果,针对于所求的两种情况,求出对应的点的坐标.
点评:先求轨迹的方程,再利用方程来解决直线与圆锥曲线的问题,是解析几何中常见的一种题型,本题所给的求轨迹的方法是定义法,这样可以减少题目的运算量,注意设直线的方程时,要讨论直线的斜率不存在的情况.

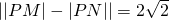 ,记动点P的轨迹为W.
,记动点P的轨迹为W. ,求直线l的方程.
,求直线l的方程. ,若
,若 =
= ,求P点坐标.
,求P点坐标.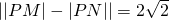 ,知点P的轨迹是以M(-2,0),N(2,0)为焦点,
,知点P的轨迹是以M(-2,0),N(2,0)为焦点, 的双曲线.
的双曲线.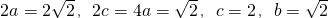
 ),B(2,-
),B(2,- ),|AB|=2
),|AB|=2 满足题意;
满足题意;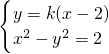 ,?(1-k2)x2+4k2x-4k2-2=0
,?(1-k2)x2+4k2x-4k2-2=0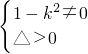 ?k∈R且k≠±1
?k∈R且k≠±1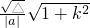
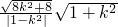 =2
=2 ?k=0即l:y=0
?k=0即l:y=0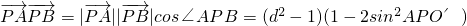
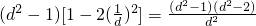 =
=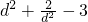
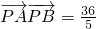 知5d4-51d2+10=0
知5d4-51d2+10=0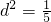 或10
或10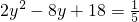 或2y2-8y+18=10
或2y2-8y+18=10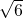 即P(
即P(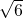 ,2)
,2)

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案