

解析:(1)因为四边形ABCD内接于圆,所以∠ABC +∠ADC = 180°,连接AC,由余弦定理:
AC2 = 42 + 62 2×4×6×cos∠ABC = 42 + 22 2×2×4 cos∠ADC.
所以cos∠ABC =![]() ,∵∠ABC∈(0,
,∵∠ABC∈(0,![]() ),故∠ABC = 60°.
),故∠ABC = 60°.
S四边形ABCD = ![]() ×4×6×sin60°+
×4×6×sin60°+![]() ×2×4×sin120°= 8
×2×4×sin120°= 8![]() (万平方米).………………4分
(万平方米).………………4分
在△ABC中,由余弦定理:
AC2 = AB2 + BC 2 2AB?BC?cos∠ABC
= 16 + 36 2×4×6×![]() .
.
AC = ![]() .…………………………6分
.…………………………6分
由正弦定理![]() ,
,
∴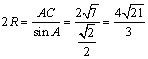
∴![]() (万米).………………8分
(万米).………………8分
(2)∵S四边形APCD = S△ADC + S△APC
又S△ADC = ![]() AD?CD?sin120°= 2
AD?CD?sin120°= 2![]() ,
,
设AP = x, CP = y.
则S△APC = ![]() .……………………10分
.……………………10分
又由余弦定理AC2 = x2 + y2 2xy cos60°
= x2 + y2 xy
= 28.
∴x2 + y2 xy≥2xy xy = xy.
∴xy≤28 当且仅当x = y时取等号……………………12分
∴S四边形APCD = 2![]() +
+ ![]()
∴最大面积为9![]() 万平方米.…………………………13分.
万平方米.…………………………13分.


科目:高中数学 来源: 题型:
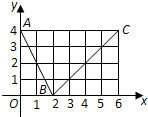 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com