
 已知F1,F2是椭圆
已知F1,F2是椭圆| x2 |
| 2 |
| y2 |
| 4 |
| PF1 |
| PF2 |
| x2 |
| 2 |
| y2 |
| 4 |
| 4-2 |
| 2 |
| 2 |
| 2 |
| PF1 |
| PF2 |
| x2 |
| 2 |
| y2 |
| 4 |
| 2 |
| 2 |
| 2 |
| 2 |
|
| 2 |
| 2 |
-2k(
| ||
| 2+k2 |
k2-2
| ||
| 2+k2 |
2
| ||||
| 2+k2 |
k2+2
| ||
| 2+k2 |
2
| ||||
| 2+k2 |
| yA-yB |
| xA-xB |
| 2 |
| 2 |
|
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| m2-4 |
| 4 |
| (1+2)((x1+x2)2-4x1x2) |
3(
|
| |m| | ||
|
| 1 |
| 2 |
|
| 2 |
| 2 |
| 2 |
| 2 |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
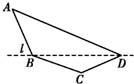 某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).
某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).| sinA |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
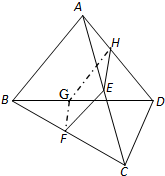 如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.
如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.| d1 |
| d2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 27 |
| 2 |
| 2 |
(lg
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com