
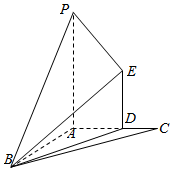
 平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;分析 (1)延长PE交AC于F,可证F与C重合,故直线BC即为面PBE与面ABC的交线;
(2)以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出面PBE与面ABC所成的锐二面角的大小.
解答 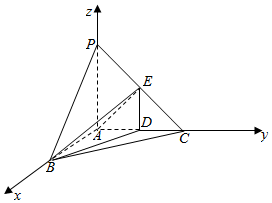 解:(1)延长PE交AC于F,直线BC即为面PBE与面ABC的交线;
解:(1)延长PE交AC于F,直线BC即为面PBE与面ABC的交线;
理由如下:
∵AP、AB、AC两两互相垂直,
∴PA⊥平面ABC,
∵DE⊥平面ABC,
∴DE∥PA,
∴$\frac{DF}{AF}$=$\frac{DE}{PA}=\frac{1}{2}$,
∴F与C重合.
∵C∈PE,C∈AC,PE?平面PBE,AC?平面ABC,
∴C是平面PBE和平面ABC的公共点,
又B是平面PBE和平面ABC的公共点,
∴BC是面PBE与面ABC的交线.
(2)∵AP、AB、AC两两互相垂直,
∴AB⊥平面PAC,∴VB-PADE=$\frac{1}{3}$S梯形ADEP•AB=$\frac{1}{3}$(1+2)×1×AB=$\frac{\sqrt{3}}{3}$,解得AB=$\frac{2\sqrt{3}}{3}$.
以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,
B($\frac{2\sqrt{3}}{3}$,0,0),P(0,0,2),E(0,1,1),
$\overrightarrow{PB}$=($\frac{2\sqrt{3}}{3}$,0,2),$\overrightarrow{PE}$=(0,1,-1),
设二面角PBE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=\frac{2\sqrt{3}}{3}x+2z=0}\\{\overrightarrow{n}•\overrightarrow{PE}=y-z=0}\end{array}\right.$,取y=1,得$\overrightarrow{n}$=(-$\sqrt{3}$,1,1),
平面ABC的法向量$\overrightarrow{m}$=(0,0,1),
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∴面PBE与面ABC所成的锐二面角的大小为arccos$\frac{\sqrt{5}}{5}$.
点评 本题考查了平面的性质,二面角的计算,属于中档题,解题时要认真审题,注意向量法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 偏爱蔬菜 | 偏受肉类 | 合计 | |
| 五十岁以下 | |||
| 五十岁以上 | |||
| 合计 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x+3 | B. | y=2x-1 | C. | y=-6x+7 | D. | y=3x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=ln|x| | C. | y=sin($\frac{π}{2}$-x) | D. | y=-x2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均每天锻炼 的时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
| 总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 20 | 110 | |
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
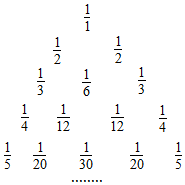 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com