Question

已知x∈（-1，2），则f（x）=-4^x+2^x+1+1的值域为________．

Answer 1

（-7，2]
分析：先进行换元，令t=2^x，由x∈（-1，2）可得，然后对函数配方找出对称轴，而＜t＜4，利用对称轴与区间的位置关系求出最小值．
解答：∵x∈（-1，2）
令t=2^x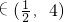
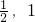
∵y=-4^x+2^x+1+1=-t²+2t+1=-（t-1）²+2在（）单调递增，[1，4）单调递减
当t=1即x=0时函数有最大值2
当x=4时，函数有最小值-7
所以函数的值域为（-7，2]
故答案为：（-7，2]
点评：本题以指数函数为载体考查二次函数的值域，属于求二次函数的最值问题，属于基本题．