练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数，若在（0，+）上恒成立，求的取值范围。
    因为在（0，+）上恒成立，即
    ∴           ∵ 的最小值为4      ∴ 
    解得
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    甲、乙两地相距S千米，汽车从甲地匀速驶到乙地，速度不得超过c千米/小时，已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成，可变部分与速度v(km/h)的平方成正比，比例系数为b,固定部分为a元 
    (1)把全程运输成本y(元)表示为v(km/h)的函数，并指出这个函数的定义域；
    (2)为了使全程运输成本最小，汽车应以多大速度行驶？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知一动直线与两坐标轴的正半轴围成的三角形的面积的数值比直线的纵、横截距之和大1，求这三角形面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

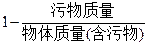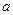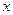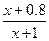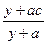    对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为:)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为(1≤a≤3).设用单位质量的水初次清洗后的清洁度是(),用质量的水第二次清洗后的清洁度是,其中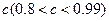是该物体初次清洗后的清洁度.
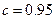    (Ⅰ)分别求出方案甲以及时方案乙的用水量,并比较哪一种方案用水量较少;
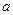    (Ⅱ)若采用方案乙,当为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论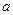取不同数值时对最少总用水量多少的影响.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某公司租地建仓库，每月土地占用费y1与车库到车站的距离成反比，而每月库存货物的运费y2与到车站的距离成正比，如果在距车站10公里处建仓库，这两项费用y1和y2分别为2万元和8万元，那么要使这两项费用之和最小，仓库应建在离车站__________公里处 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设若是与的等比中项，则的最小值为（   ）
    A．2B．C．4D．8

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若不等式对任意的、恒成立，则正实数的最小值为
    A．1B．4C．9D．14

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

     
                 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若，全集，则___________ 
     

    查看答案和解析>>

    同步练习册答案