
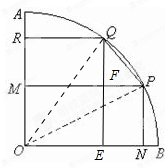
 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.| (QR+MP)×RM |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| (QR+MP)×RM |
| 2 |
(2cosα+
| ||||
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1-t2 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| an | ||
2kn-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
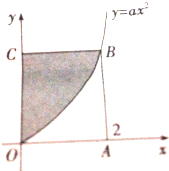 如图,长方形的四个顶点为O(0,0),A(2,0),B(2,4),C(0,4)曲线y=ax2经过点B,现将一质点随机投入正方形OABC中,则质点落在图中阴影区域的概率是
如图,长方形的四个顶点为O(0,0),A(2,0),B(2,4),C(0,4)曲线y=ax2经过点B,现将一质点随机投入正方形OABC中,则质点落在图中阴影区域的概率是查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com