
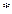 表示名额.如
表示名额.如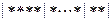
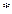 ”与每个“
”与每个“ ”都视为一个位置,由于左右两端必须是“|”,故不同的分配方法相当于
”都视为一个位置,由于左右两端必须是“|”,故不同的分配方法相当于 个位置(两端不在内)被2个“|”占领的一种“占位法”.
个位置(两端不在内)被2个“|”占领的一种“占位法”.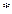 ”之间的23个空隙中选出2个空隙插入“|”,故有
”之间的23个空隙中选出2个空隙插入“|”,故有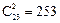 种.
种. ,则每校至少有一个名额的分法数为不定方程
,则每校至少有一个名额的分法数为不定方程 .
. 的非负整数解的个数,它等于3个不同元素中取21个元素的可重组合:
的非负整数解的个数,它等于3个不同元素中取21个元素的可重组合: .
.

科目:高中数学 来源:不详 题型:单选题
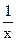 ∈A,就称A是伙伴关系集合,集合M={-1,0,
∈A,就称A是伙伴关系集合,集合M={-1,0,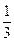 ,
,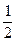 ,1,2,3,4}的所有非空子集中,具有伙伴关系的集合的个数为:
,1,2,3,4}的所有非空子集中,具有伙伴关系的集合的个数为:| A.15 | B.16 | C.28 | D.25 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.70种 | B.72种 | C.76种 | D.78种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.540 | B.300 | C.150 | D.180 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com