


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆八中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:重庆八中2011-2012学年高三上学期第一次月考(数学文) 题型:解答题
(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
卫生部门对某大学的4个学生食堂进行食品卫生检查(简称检查).若检查不合格,则必须整改,若整改后经复查不合格则强行关闭该食堂.设每个食堂检查是否合格是相互独立的,且每个食堂整改前检查合格的概率为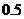 ,整改后检查合格的概率是
,整改后检查合格的概率是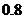 .计算(结果用小数表示,精确到
.计算(结果用小数表示,精确到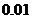 )
)
(Ⅰ)恰有一个食堂必须整改的概率;
(Ⅱ)至少关闭一个食堂的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com