
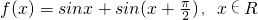 .
. …..(2分)
…..(2分)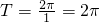 …(4分)
…(4分) ,此时x+
,此时x+ =2kπ+
=2kπ+ ,k∈Z,x的取值集合是
,k∈Z,x的取值集合是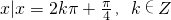 ….(6分)f(x)的最小值
….(6分)f(x)的最小值 ,此时x+
,此时x+ =2kπ-
=2kπ- ,k∈Z,x的取值 x的取值集合是
,k∈Z,x的取值 x的取值集合是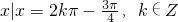 …..(8分)
…..(8分) x+ | 0 |  | π |  | 2π |
| x | - |  |  |  |  |
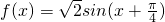 | 0 |  | 0 | - | 0 |
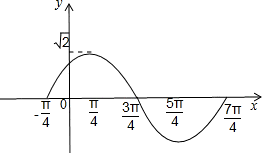
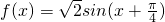 后,
后, 看作整体,令x+
看作整体,令x+ 取0,
取0,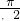 ,π,
,π, ,2π,并求出对应的x的值,列表,用五点画图法画出函数图象即可.
,2π,并求出对应的x的值,列表,用五点画图法画出函数图象即可.

科目:高中数学 来源:2012届丹东市四校协作体高三摸底测试数学(零诊) (文) 题型:解答题
(本小题满分12分)已知函数 .
.
(I)当 时,若函数
时,若函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(II)若 ,
, ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求 和
和 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省临沂市临沭县高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州市高三(上)12月质量检查数学试卷(文科)(解析版) 题型:解答题
 .
. ,,求△ABC的面积.
,,求△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com