
已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且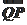 ·
·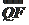 =
=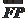 ·
·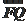 .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1,|DB|=l2,求+的最大值.
解:(1)设P(x,y),则Q(x,-1),
∵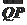 ·
·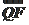 =
=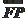 ·
·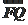 ,
,
∴(0,y+1)·(-x,2)=(x,y-1)·(x,-2).
即2(y+1)=x (y-1),即x2=4y,
所以动点P的轨迹C的方程为x2=4y.……………………………………………4分
(2)设圆M的圆心坐标为(a,b),则a2=4b. ①
圆M的半径为|MD|=.
圆M的方程为(x-a)2+(y-b)2=a2+(b-2)2.
令y=0,则(x-a)2+b2=a2+(b-2)2,
整理得,xax+4b-4=0. ②
由①、②解得x=a±2.
不妨设A(a-2,0),B(a+2,0),
∴l1=,l2=.
∴+==
=2=2, ③
当a≠0时,由③得,+=2≤2=2.
当且仅当a=±2时,等号成立.
当a=0时,由③得,+=2.
故当a=±2时,+的最大值为2.………………………………………10分


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
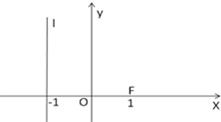 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且 |
| OP |
 |
| QF |
 |
| FP |
 |
| FQ |
 |
| MA |
 |
| AF |
 |
| MB |
 |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
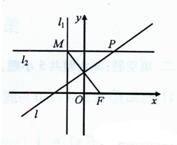 已知点F(1,0)和直线l1:x=-1,直线l2过直线l1上的动点M且与直线l1垂直,线段MF的垂直平分线l与直线l2相交于点P.
已知点F(1,0)和直线l1:x=-1,直线l2过直线l1上的动点M且与直线l1垂直,线段MF的垂直平分线l与直线l2相交于点P.| NP |
| NQ |
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省米易中学高一下学期1月月考数学理卷 题型:解答题
已知点F(0, 1),直线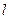 :
: 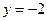 ,圆C:
,圆C: 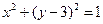 .
.
(Ⅰ) 若动点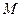 到点F的距离比它到直线
到点F的距离比它到直线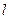 的距离小1,求动点
的距离小1,求动点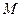 的轨迹E的方程;
的轨迹E的方程;
(Ⅱ) 过轨迹E上一点P作圆C的切线,切点为A、B,当四边形PACB的面积S最小时,求点P的坐标及S的最小值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省高一下学期1月月考数学理卷 题型:解答题
已知点F(0, 1),直线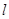 :
: 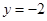 ,圆C:
,圆C: 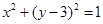 .
.
(Ⅰ) 若动点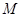 到点F的距离比它到直线
到点F的距离比它到直线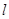 的距离小1,求动点
的距离小1,求动点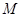 的轨迹E的方程;
的轨迹E的方程;
(Ⅱ) 过轨迹E上一点P作圆C的切线,切点为A、B,当四边形PACB的面积S最小时,求点P的坐标及S的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com