
一个三条侧棱两两互相垂直并且侧棱长都为1的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为 ( 。 )
A. B.
B.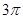 C.
C.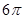 D.
D.
科目:高中数学 来源: 题型:
| 6 |
查看答案和解析>>
科目:高中数学 来源:江苏省赣榆高级中学2007-2008学年度高三第三次阶段考试数学试题(理) 题型:022
现有一块正三棱锥形石料,其三条侧棱两两互相垂直,且侧棱长为1 m,若要将这块石料打磨成一个石球,则所得石球的最大半径为________
查看答案和解析>>
科目:高中数学 来源:2012-2013学年东北三省四市教研协作体高三等值诊断联合(长春三模)文数学(解析版) 题型:选择题
一个三条侧棱两两互相垂直并且侧棱长都为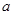 的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )
的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )
A.  B.
B.
 C.
C.
 D.
D.
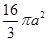
查看答案和解析>>
科目:高中数学 来源:福建省厦门六中09-10学年高二下学期期中考试(理) 题型:解答题
如图,在直角三角形ABC中,AD是斜边BC上的高,有很多大家熟悉的性质,例如“AB⊥AC”,勾股定理“|AB|2+|AC|2=|BC|2”和“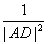 =
=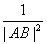 +
+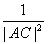 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
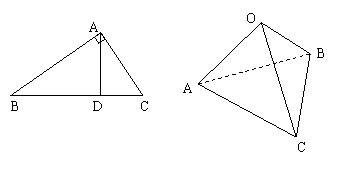 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com