练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数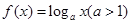的图象经过区域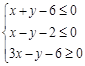，则a的取值范围是（   ）

    A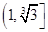．B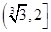．C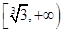．D．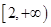

    C

    解析考点：二元一次不等式（组）与平面区域；对数函数的图像与性质．
    专题：数形结合．
    分析：先依据不等式组 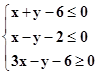，结合二元一次不等式（组）与平面区域的关系画出其表示的平面区域，再利用函数f（x）=logax（a＞1）的图象特征，结合区域的角上的点即可解决问题．
    解答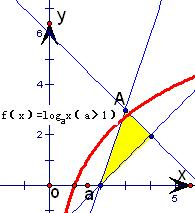：解：作出区域D的图象，图中阴影部分．
    联系函数f（x）=logax（a＞1）的图象，能够看出，
    当图象经过区域的边界点A（3，3）时，a可以取到最小值：，
    而显然只要a大于，
    函数f（x）=logax（a＞1）的图象必然经过区域内的点．
    则a的取值范围是（，+∞]
    故选C．
    点评：这是一道略微灵活的线性规划问题，本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质，本题的注意点是要用运动的观点看待问题，应用简单的转化思想和数形结合的思想解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2006•静安区二模）某种洗衣机在洗涤衣服时，需经过进水、清洗、排水、脱水四个连续的过程．假设进水时水量匀速增加，清洗时水量保持不变．已知进水时间为4分钟，清洗时间为12分钟，排水时间为2分钟，脱水时间为2分钟．洗衣机中的水量y（升）与时间x（分钟）之间的关系如下表所示：
    x 0 2 4 16 16.5 17 18 …
    y 0 20 40 40 29.5 20 2 …
    请根据表中提供的信息解答下列问题：
    （1）试写出当x∈[0，16]时y关于x的函数解析式，并画出该函数的图象；
    （2）根据排水阶段的2分钟点（x，y）的分布情况，可选用y=
    a
    x
    +b    或y=c（x-20）2+d（其中a、b、c、d为常数），作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数．试分别求出这两个函数的解析式；
    （3）请问（2）中求出的两个函数哪一个更接近实际情况？（写出必要的步骤）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•宝坻区一模）已知函数f（x）=ax3+bx2的图象经过点A（1，4），且在点A处的切线恰好与直线9x-y+3=0平行．
    （Ⅰ）求实数a，b的值；
    （Ⅱ）若函数f（x）在区间[m，m+1]上单调递增，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•花都区模拟）已知函数f（x）=ax+b（a＞0）的图象经过点（2，3）和原点，则f（-2）=
    -
    3
    4
    -
    3
    4
    ．

    查看答案和解析>>

    同步练习册答案