
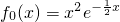 ,记f0(x)的导函数f'0(x)=f1(x),f1(x)的导函数f'1(x)=f2(x),f2(x)的导函数f'2(x)=f3(x),…,fn-1(x)的导函数f'n-1(x)=fn(x),n=1,2,….
,记f0(x)的导函数f'0(x)=f1(x),f1(x)的导函数f'1(x)=f2(x),f2(x)的导函数f'2(x)=f3(x),…,fn-1(x)的导函数f'n-1(x)=fn(x),n=1,2,…. x2+2x)e
x2+2x)e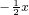 ,
, x2-2x+2)e
x2-2x+2)e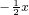 ,
, x2+
x2+ x-3)e
x-3)e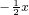 ,
,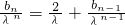 ,其中n=1,2,…,
,其中n=1,2,…,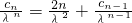 ,其中n=1,2,…,
,其中n=1,2,…, 代入得:fn(0)=n(n-1)(-
代入得:fn(0)=n(n-1)(- )n-2.其中n∈N.
)n-2.其中n∈N. )n-1,
)n-1,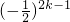 <0,
<0, ,f2k+1(0)=2k(2k+1)
,f2k+1(0)=2k(2k+1)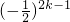 ,
, +2k(2k+1)
+2k(2k+1)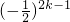 =(2k+1)(k-1)
=(2k+1)(k-1)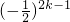 <0,
<0,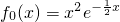 ,利用导数的性质,能够依次求出f1(x),f2(x),f3(x)的表达式即可得到f3(0).
,利用导数的性质,能够依次求出f1(x),f2(x),f3(x)的表达式即可得到f3(0). 代入即得:fn(0);
代入即得:fn(0); )n-1,再对n分奇偶数讨论:当n=2k(k=1,2,…)时,得到当Sn最大时,n为奇数.当n=2k+1(k≥2)时,数列{S2k+1}是递减数列,又S1=f2(0),S3=f2(0)+f3(0)+f3(0)=2,从而得出当n=1或n=3时,Sn取最大值.
)n-1,再对n分奇偶数讨论:当n=2k(k=1,2,…)时,得到当Sn最大时,n为奇数.当n=2k+1(k≥2)时,数列{S2k+1}是递减数列,又S1=f2(0),S3=f2(0)+f3(0)+f3(0)=2,从而得出当n=1或n=3时,Sn取最大值.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:江门二模 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com